|
Interactive animations
Basic story, without math
Coriolis effect related
Rotation
Fundamentals
Classical mechanics
Variational mechanics
General physics: rotation
Relativistic physics:
Java simulations
Created with EJS |
Numerical analysis supporting derivation of angular momentum
Two weights connected by a spring, rotating around the common center of mass, with an oscillation in distance to the center.
This page accompanies the Numerical analysis of angular momentum conservation (Excel spreadsheet, 244 KB). Following the description of the spreadsheet there is a qualitative discussion of the dynamics. Description of the spreadsheetThe method of this numerical analysis is leapfrog integration. Professor Michael Fowler has described the method of Leapfrog integration with the use of a spreadsheet. See also Michael Fowler's Teaching Dynamics with Excel97. This spreadsheet, Numerical analysis of angular momentum conservation, is set up to calculate the energy conversions of the two weights in the animation. Therefore in this spreadsheet the restoring force is a harmonic force, but any force law that is a function of of radial distance can be inserted, for example the inverse square law of gravitation. The mass of the rotating object is taken as one unit of mass. The initial radius is set at one unit of length. If the initial angular velocity is set at one unit (one radial per unit of time), then the ensuing motion is circular. If a larger or smaller initial angular angular velocity is inserted, the resulting motion is ellipse-shaped, like the motion depicted in the animation. The definition of the "required force" of column H is as follows: Column A of the spreadsheet defines the time increments. In column B, radial velocity, I only used data from the row above it. The change of radial velocity, Δv, is calculated by subtracting the required force from the actual force, and multiplying that with Δt, the time increment. In column C, Δr, I multiplied the radial velocity with the time increment. In column D, radius, I added the radial increment to the previous radius. In column E, the centripetal force is defined. In this case a harmonic force is defined: the restoring force is directed inwards, and it is proportional to the radial distance. Column F deals with the total energy and work. The centripetal force is doing work, either positive work or negative work, causing an increase and a decrease of the total kinetic energy respectively. Enew = Eold + (F In column G, I calculated the rotational kinetic energy by subtracting from the total kinetic energy the energy that corresponds to the radial velocity. The angular velocity then follows from the rotational kinetic energy. This is the following formula: In column H, I calculated the required centripetal force, using the angular velocity and the radius of the same row. Finally, in column I, the angular momentum is calculated. As predicted analytically, the angular momentum turns out to be conserved. With the time increment at 0.01, there is a small fluctuation in the angular momentum. When smaller time increments are taken, the approximation is closer, and the fluctuation in the numerical calculation of the angular momentum is less. Column L shows that the oscillation in kinetic energy is a harmonic oscillation; the remainder after subtracting it from a cosine fucntion is practically zero. Emergent propertyIn this spreadsheet calculation, conservation of angular momentum appears as an emergent property. That is, conservation of angular momentum can be seen as a consequence of the laws of physics that were applied to perform the calculation: Conservation of energy, work, Newtons second law, and symmetry of the laws of physics for all direction. This illustrates a very general property of logical systems: there is great freedom to exchange axiom and theorem without altering the system's content. Another emergent property is the time it takes for a full cycle. After 628 time increments of 0.01 second, the process has gone through a whole cycle. Hence a full cycle takes 6.28 seconds. This coincides with the period of revoltution as predicted analytically: the number pi multiplied by two. Advantage of focusing on energy conversion
Over time, some of the energy will dissipate, leaving a rotation with constant radial distance and constant angular velocity.
In the case of the two weights orbiting each other, focusing on the energy conversions is far more informative than focussing on conservation of angular momentum. As long as there is oscillation between contraction and extension, there is opportunity for dissipation of energy. Due to internal friction of the spring energy dissipates, and the final state is a rotation with constant radial distance. Clearly, the final state is a state of some sort of equilibrium, but it is not an equilibrium of forces. Instead, the final state is a state of equilibrium between two repositories of energy. The oscillation between contraction and extension is an oscillation between rotational kinetic energy and potential energy. The transferring agent between the two energies is radial velocity. Internal friction of the spring dissipates energy, and in the final state both energies are constant, and they are equal to each other. The fact that in the equilibrium state the two energies are equal to each other is reminiscent of the equipartition theorem of thermodynamics. In a state of energy equilibrium the total energy is distributed equally over the available degrees of freedom of the system. Qualitative discussion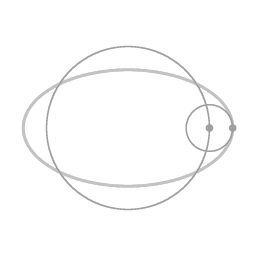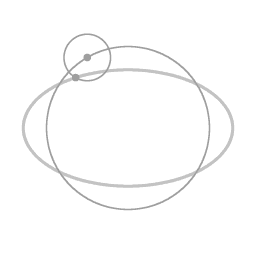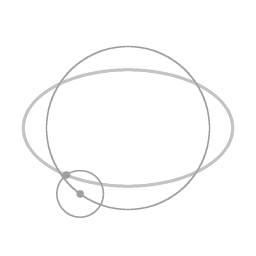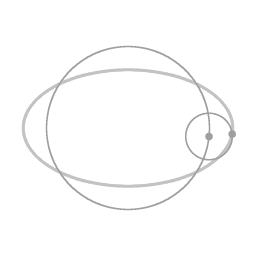
Diagram 1.
The point where the object is farthest away from the center of rotation. 
Diagram 2.
Along the trajectory from diagram 1 to diagram 2, the centripetal force has been increasing the inward radial velocity and the angular velocity. Up to diagram 2, the actual centripetal force was stronger than the required centripetal force. 
Diagram 3.
Along the trajectory from diagram 2 to diagram 3, the actual centripetal force is less than the required centripetal force, so from 2 to 3, the inward radial velocity is decreasing. From 2 to 3, the angular velocity keeps increasing. 
Diagram 4.
Along the trajectory from diagram 3 to diagram 4, an outward velocity is building up, at the expense of angular velocity. 
Diagram 5.
Along the trajectory from diagram 4 to diagram 5, the outward radial velocity is reduced to zero, and the angular velocity is decreased.
|
