This article is a barebone introduction. I don't present any mathematics here, only lots of diagrams and animations. The other articles on this site do have the math content to prove the statements that are made. Here you'll have to take my word for it.
The Coriolis effect in Meteorology
On this page I discuss the rotation-of-Earth-effect that is taken into account in Meteorology, where it is referred to as 'the Coriolis effect'. (For the rotation of Earth effect that applies in ballistics, see the following two Java simulations: Great circles and Ballistics).
The rotating Earth
A key consequence of the Earth's rotation is the deviation from perfectly spherical form: there is an equatorial bulge. The bulge is small; on Earth pictures taken from outer space you can't see it. It may seem unimportant but it's not: what matters for meteorology is an effect that arises from the Earth's rotation and Earth's oblateness together.
A model: parabolic dish
Thinking about motion over the Earth's surface is rather complicated, so I turn now to a model that is simpler but still presents the feature that gives rise to the Coriolis effect.

The dish in the picture is used by students of Geophysical Fluid Dynamics for lab exercises. This dish was manufactured as follows: a flat platform with a rim was rotating at a very constant angular velocity (10 revolutions per minute), and a synthetic resin was poured onto the platform. The resin flowed out, covering the entire area. It had enough time to reach an equilibrium state before it started to set. The surface was sanded to a very smooth finish.
Also, note the construction that is hanging over the dish. The vertical rod is not attached to the table but to the dish; when the dish rotates the rod rotates with it. The overhanging construction carries a video camera so the footage from that camera will show the motion as seen from a co-rotating point of view.
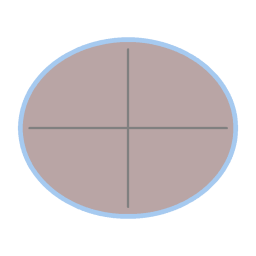
It can be shown mathematically that the cross-section of the resulting surface is a parabola. Here is how that parabolic dish serves as a model for the rotating Earth: If you pour water out on the dish (while it is rotating at the same 10 revolutions per minute) you get a water layer with an even thickness; the equilibrium shape of that water is the same as the equilibrium shape of the poured out resin.

|
|
|
The natural shape of a liquid surface is to be flat. Due to the rotation the liquid surface assumes a parabolic shape. |
The natural shape of a planet is to be spherical. Due to the rotation the Earth has an oblate shape, with the water as a layer a couple of kilometers thick. |
Incidentally, the Earth didn't get to its present oblate shape from a spherical shape. The preceding form, way in the beginning of our solar system, was a protoplanetary disk. Under its self-gravity the protoplanetary disk contracted more and more, eventually resulting in a planet. Because of the rotation the contraction did not proceed all the way to a spherical shape.
Dish and hemisphere
The parabolic dish is hollow, and the Earth is convex, and recognizing that the parabolic dish models the Earth is not straightforward. The following series of four images is designed to bridge the gap.
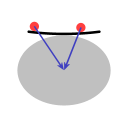
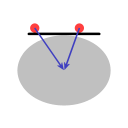
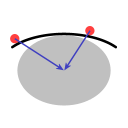
Image A shows that if a dish as big as a continent would be placed on the north pole then the Earth's gravity would tend to pull objects on the dish towards the middle.
In Image B the straight line represents a huge perfectly flat disk. Even though it is flat, the fact that the Earth's gravity pulls towards the Earth's center gives all objects on the disk a tendency to move to the middle.
In Image C the line represents a structure that has in common with the previous two examples that objects located on it will tend to move to the middle. Even though the structure is convex, it is effectively a bowl because the outside, the rim, is further away from the Earth's center of gravity than the middle.
Finally, Image D represents the situation on Earth, with its equatorial bulge. Effectively, each hemisphere is a bowl, and the equator is the rim of these bowls.
Force
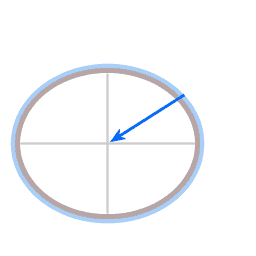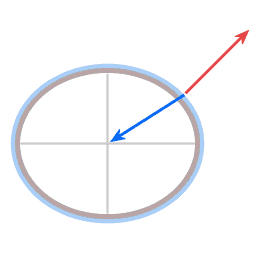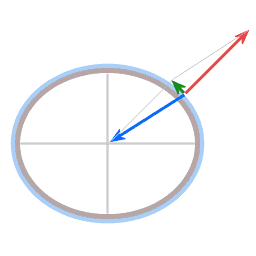
In both diagrams the blue arrow represents gravity. In the case of the dish it pulls straight down, in the case of the planet it pulls towards the planet's center.
The red arrow represents height sustaining force. (Height sustaining force, whenever it is present, acts perpendicular to the local level surface.)
Everything on Earth is at all times subject to both these forces: gravity and height sustaining force. If you are standing on solid ground the structural integrity of the solid ground keeps you from sinking towards the Earth's center. If you are floating the buoyancy force is providing the height sustaining force. An airship (a Zeppelin) floats; the air mass around it is providing the buoyancy force. In the case of an airplane the lift generated by the wings provides the height sustaining force.
There is one specific circumstance such that for a particular object no height sustaining force is present: during free fall. If you throw a ball then during its flight the ball is not subject to a height sustaining force (in cases where air resistence is negligable).
Resultant force
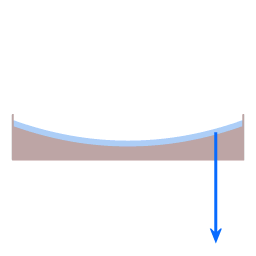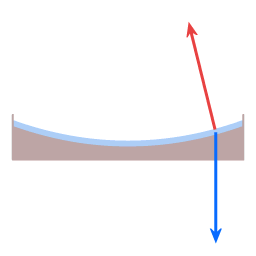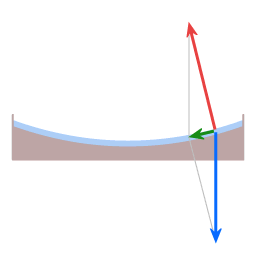
In both cases here, dish and Earth, the height sustaining force and gravity are not exactly opposite in direction. The angle between them gives rise to a resultant force (green arrow), acting towards the center of rotation.
(For some remarks about how large the Earth's equatorial bulge is, and how large the inward force is, see the Equatorial bulge discussion on this page.)
An object located on the parabolic dish
This particular dish doesn't get water poured over it, that would make it too heavy. What is done instead for demonstrations is that small objects, manufactured to have very little friction, are placed on the surface.
Co-moving

In the above animation two perspectives are shown next to each other. On the left the actual motion of the dish, on the right the motion as seen from the overhanging video-camera. On the rim of the disk different shades of grey divide the rim in four quadrants, to show clearly which view is the non-rotating view.
In the above view the frictionless object has been placed on the parabolic dish in such a way that it is simply co-rotating with the dish. The dish is rotating with the same angular velocity as when it was manufactured. In that case the inward force arising from the slope is precisely the amount that is required to sustain motion along a circle. If you would place several objects on the rotating dish, all with no velocity relative to the dish, then they would simply keep their positions relative to each other. In that case if you just have the image from the overhanging camera you'd be hard pressed to tell whether you are looking at a rotating assembly or a stationary assembly.
Velocity relative to dish
When the object has a velocity relative to the rotating dish interesting things happen.
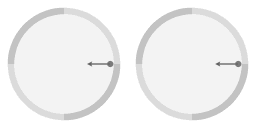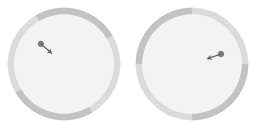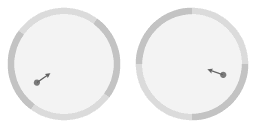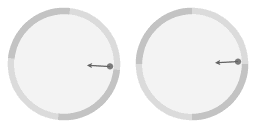
In the above animation an arrow has been added to emphasize that the slope of the surface gives rise to an inward force. Note that near the rim the inward force is stronger. In fact, it is precisely proportional; a property of the parabolic shape is that the inward force arising from the slope is exactly proportional to the distance to the central axis of rotation. From here on I will write 'proportional force' as shorthand for 'a force that is proportional to the distance to the central axis of rotation.'
Compared to the circular motion the frictionless object has been nudged; it has been given a velocity relative to the parabolic dish. Note that on average the object is still co-rotating with the dish, it's just that the circumnavigation is now not circular but ellipse-shaped.
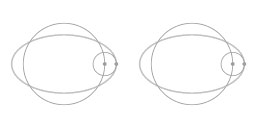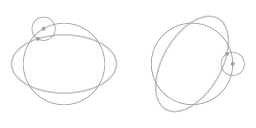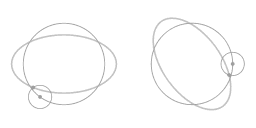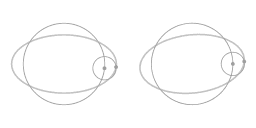
The above animation shows that the motion along the ellipse-shaped trajectory can be seen as a combination of two circles: a main circle and an epi-circle. As seen from a co-rotating view what you see is precisely the motion along the epi-circle.
The page Coriolis effect presents an interactive animated diagram; the animation has sliders, allowing the visitor to explore a variety of cases.
Rule of motion
The following statement is proved in other articles on this website, here I will just state this rule of motion:
- When the force that sustains the circumnavigating motion is proportional then the motion as seen from a co-rotating point of view is precisely the epi-circle.
Here is what is important about that rule of motion:
- As an object moves along the epi-circle it is constantly turning (and in the examples here the turn is to the right). The fact that the epi-circle is indeed a perfect circle means that the tendency to turn to the right is equally strong in all directions.
This rule of motion applies both in the case of motion over the surface of the parabolic dish and the case of motion over the Earth's surface.
Adding pressure gradient force to the picture
The lesson learned from motion on the surface of the parabolic dish can now be applied to motion over the surface of the Earth: the tendency to deflect is equally strong in all directions.
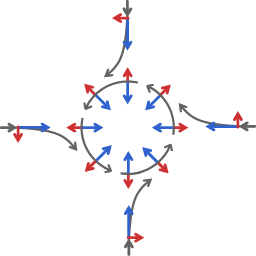
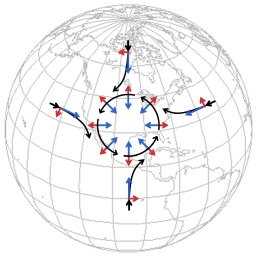
In meteorology, the two main factors affecting motion of winds are pressure gradient force and Coriolis effect. The following pictures represent the formation of flow around a low pressure area.
The blue arrows represent the tendency to flow towards a low pressure area, the red arrows represent the Coriolis effect. The diagrams are very schematic, to bring out the features that are essential.
At the start: air mass, being subject to pressure gradient force, starts flowing from all sides to the low pressure area. All the flows, from the North, the South, the East or the West, etc, get deflected to the right of their initial direction. The overall result of the deflections is that the flows shepherd each other into a flow pattern around the low pressure area. In the end the direction of flow is perpendicular to the pressure gradient.
The flow around the low pressure area is characterized by a sort of tug-of-war between pressure gradient force and Coriolis effect.
And there is another way in which the Coriolis effect remains an active factor: when the overall flow field contracts there is an inward velocity component. Every time some inward velocity component developes the Coriolis effect deflects that velocity component to flow that is once more perpendicular to the pressure gradient. So the Coriolis effect not only fosters the formation of the flow around the low pressure area, it also acts to sustain that flow.
Key points
- In the physics of the atmosphere's motions the prime influence is the force that sustains the circumnavigating motion. All air mass is at al times subject to a force towards the Earth's axis.
- Because of that force air mass that has no velocity with respect to the Earth remains co-moving with the Earth, and the direction of air mass that does have a velocity relative to the Earth is affected.
- The tendency to change direction (relative to the Earth) is the same in all directions.
Remarks
Equatorial bulge

At the equator the Earth's surface is about 20 kilometers further away from the Earth's geometric center than at the poles. Compared to the total Earth radius of 6400 kilometer that looks like a very small difference indeed, you may be tempted to think the bulge is negligable.
In the diagram: for vivid display the angle between the red and the blue arrow is exaggerated; in the case of the actual Earth that angle, at 45 degrees latitude, is about a tenth of a degree. That downward slope of 0.1 degree provides the required inward force.
At a rate of one revolution per day, how much inward force is required to circumnavigate the Earth's axis? For the latitude of 45 degrees the calculation gives that for an object with a mass of 1 kilogram a force of 1.7 gram-force is required. The ratio is 1:580. So whatever measure of weight you use, divide it by 580 and you have the required inward force.
(In case you decide to check the number I present here: the required inward force I gave is the component parallel to the local surface, as depicted in the diagram.)
I weigh about 80 kilogram (176 american pounds), and for me the required force is about 140 gram-force. If you have some weighing utensil at hand, feel how strong you have to push to exert 140 gram-force.
Cause of the turning
The cause of the turning is different in each direction, but the common factor is that in every direction it's an interplay between the inward force and the inertia of the circumnavigating object.

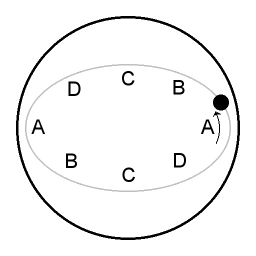
An overview:
| A | When the moving object is at the parts of the trajectory labeled A it is circumnavigating slower than the parabolic dish itself. Circumnavigating slower there is a surplus of inward force, and subsequently the object is pulled closer to the central axis. |
| C | When the moving object is at the parts of the trajectory labeled C it is circumnavigating faster than the parabolic dish itself. Now there is not enough inward force, and subsequently the object recedes from the central axis again. |
| B | During the parts of the trajectory labeled B the object is giving in to the inward pull, gaining velocity in the process. |
| D | During the parts of the trajectory labeled D the object is moving against the pull of the inward force, and accordingly the object is losing velocity. |
Explanation with motion in a straight line?
Here I discuss whether the turning that is so typical of the rotation-of-Earth-effect can also be explained with an example that is based on motion in a straight line. To do that I will discuss two cases, one with motion over a parabolic dish, and one with motion over a level surface. I will invoke the following as crucial criterium: the rotation-of-Earth-effect that is at play in the atmosphere is the same for all directions of motion.
Parabolic ice-rink
Imagine you are on a parabolic ice-rink. (That would require a very large platform. Actually, in France there is a scientific center that has a 13 meter diameter rotating tank. When that rotating water mass is in an equilibrium state you can try to freeze it, which would result in a parabolic ice-rink.)
Imagine you are on that ice-rink, co-rotating with it (and the ice-rink is rotating with the same angular velocity as when it was manufactured). You give an ice-hockey puck a push so that goes forward. That is: you push it so that it
still circumnavigates the central axis, but faster than the rink itself. The puck will then start to recede from the central axis.
Then give an ice-hockey puck a push in rearward direction: now it circumnavigates slower than the rink itself, and the puck will start to slump down towards the center.
Flat disk
Now for the same experiment conducted on the surface of a rotating flat disk. The animation below illustrates such a setup. You see several pucks being launched at the same time, all moving along the same straight line, but with different velocities.

The pucks that move in forward direction move away from the central axis. Ok, that is somewhat the same as in the parabolic dish case.
How about the puck that is moving in rearward direction? The rearward moving pucks are receding from the central axis of rotation too! They recede because they are moving along a straight line that is tangent to the circular platform. Hence on a flat disk it doesn't matter whether the pucks are moving forward or rearward, either way they are receding from the central axis of rotation.
The answer to the question is No: in Meteorology the deflection of the motion with respect to the rotating system cannot be explained with a example that is based on motion in a straight line.
Other material on this site
Further discussion of the terrestrial Coriolis effect is in the article Oceanography: Inertial oscillations
Java Applets
Relevant for Meteorology:
Relevant for ballistics:
- The Great circles simulation. As the name says, this shows motion along a great circle, over the surface of a sphere. The simulation shows simultaneously how it looks like from a stationary point of view and from a co-rotating point of view.
- The Ballistics and orbits simulation. With this simulation you can launch a projectile from anywhere on the planet, in any direction, the simulation then computes the trajectory.

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.
Last time this page was modified: December 29 2023