Spacestation Vertical throw
All motion is subject to the principle that is codified as Newton's First Law: an object that is free moving will travel in a straight line, with uniform velocity.
In science fiction movies rotation is sometimes used to create gravity inside a space station. Objects that are stationary with respect to the rotating space station will then experience a gravitational effect, as described by Newton's second law. The First Law physics comes into play when an object is thrown. If you throw an object, and you want it to land right at your feet again, in what direction do you need to aim?
When an object is thrown from some point inside a rotating spacestation, there are two contributions to its overall velocity:
- The velocity the particle already has as it is co-rotating with the space station.
- Additional velocity imparted by throwing.
If you want to hit something at the hub of the rotating space station, or just move through the hub area, then the throw must cancel all the pre-existing velocity.
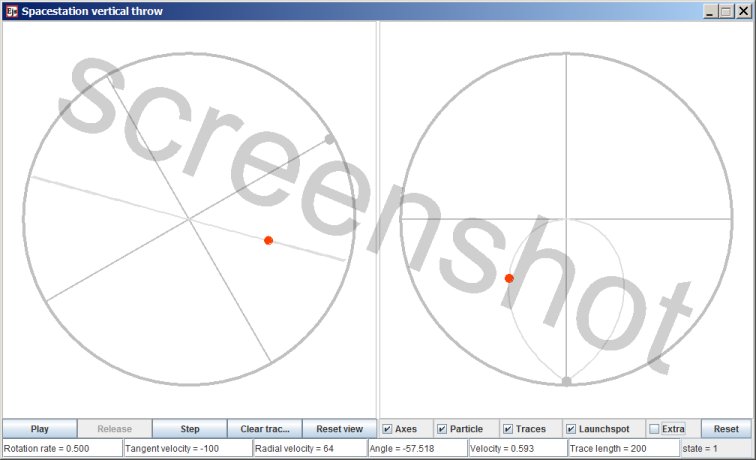
The left panel shows the motion as seen from an inertial point of view. The grey straight lines can be thought of as the axes of a coordinate system that is co-rotating with the space station, or as spokes of the space station's internal structure.
The animation's controls
The input fields
- Rotation Rate The rotation rate of the space station in radians per second.
- Tangent Velocity The tangential component of the launch velocity, relative to the space station. The value in the input field is a percentage: the percentage of co-rotating motion. A value of -100 means that the velocity from co-rotating motion is precisely cancelled by the tangential velocity from the throw.
- Radial velocity The radial component of the launch velocity, relative to the space station. When the launch angle is 45 degrees radial velocity and tangential velocity values are equal
- Launch angle The direction, in degrees, in which the object is launched. Radial direction, towards the center, is an angle of zero. Only inward angles are permitted; the input field will only accept values between -90 and 90.
- Velocity The total velocity relative to the space station, in units per second. If the space station has a radius of 100 meters then a value of 0.5 corresponds to 50 meters per second.
- Trace length If you enter an inadmissible value, such as a negative number, the trace will keep building up.
- State This non-editable field shows the current state. '0' is that the object is co-moving with the perimeter, 1 is that it will relaunch from a fixed launch spot, '2' is that the object will rebound on reaching the perimeter.
When you alter an input value you will see that one or more of the other values change also. These updates are necessary to keep the simulation in an overall consistent state.
You can change any input value while the animation is playing - no need to pause it - but generally you will see some angle in the trace. After the next relaunch or bounce the trajectory will be regular again.
The extra settings
Among the checkboxes there is also a checkbox 'Extra', which opens a small window with additional checkboxes.
- Repetitive The default setting of 'Repetitive' is that it's switched on, and then the simulation will automatically relaunch when the previously launched object hits the perimeter. When unchecked the simulation will halt when the perimeter is reached.
- Bouncing The unchecked default setting has the object relaunching from a spot that is fixed with respect to the rotating system. Bouncing is literally that: the object will simply rebound at the perimeter.
- Attempt continuous trace Generally what you will see is that the existing trace is erased on each relaunch. But if the particle hits very close to the launch spot the trace will be preserved; a continuous trace. When unchecked the trace will always be erased between launches.
- Left panel visible You can blank the left panel if you feel watching both panels simultaneously is rather busy.
- Right panel visible Idem.
Method of computation
First the motion with respect to the inertial coordinate system is calculated. Subsequently the x and y values are transformed to positions relative to the co-rotating coordinate system.
The calculation of the rebounds is technically incorrect. It ought to be treated as a reflection, with the reflection angle computed to be equal to the incidence angle. Now, because of the symmetry of a circle, when bouncing around inside it the incidence angle will always be equal to the reflection angle of the previous rebound. So rather than computing the new reflection angle the angle of the original launch is reused (incidental advantage: there won't be accumulation of error.)
Technical details
This simulation has been created with EJS
EJS stores the specifications of a simulation in a plain text file, with extension .xml
You can examine how the simulation has been set up by opening the simulation .xml file with EJS.
Download location for the EJS software
Download location for the Spacestation vertical throw source file
(The file is zipped because a browser will attempt to parse any .xml file.)

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.
Last time this page was modified: June 18 2017