Coriolis effect

This animation forms part of a pair of rotation effect animations that complement each other. The other rotation effect animation is called centrifugal effect.

This animation focuses on the underlying characteristic that the various cases where the Coriolis effect is at play have in common.

Rotational-vibrational coupling
The fluid dynamics of Meteorology and Oceanography
The Foucault pendulum

The above cases and others are discussed in separate articles. For a first introduction to the physics of atmosphere and its winds go to the rotation of Earth effect that is taken into account in Meteorology.

Also available: a 3D simulation (Java applet), called inertial oscillation, which presents the rotation-of-Earth effect that is essentially the same as the rotation effect in this animation.

View

The two circles with quadrants represent a disk. The left view shows the disk from a stationary point of view. The view on the right is the same disk, as seen from a co-rotating point of view. It's the view you would get if a video camera is suspended above the disk, co-rotating with it.

The green arrow represents a force that is acting upon the moving object, sustaining a state of circumnavigating motion. The force represented with the green arrow is set up to have the following properties: it is at all times pointing towards the same center, and the strength increases in proportion with the distance to the center. That is, at twice the distance the force is twice as strong. I will refer to these properties as: 'proportional centripetal force'. The resulting motion has the following symmetry: the period of the oscillation is independent of the amplitude. The rotation rate of the disk with the 4 quadrants matches that consistent period of circumnavigation.

Controlling the animation

The two elements underneath the two disks are sliders. While the animation is playing the two sliders are temporarily not displayed. The slider on the left directs the (average) distance of the object to the center of circumnavigation, the slider on the right directs the difference in amplitude between the x-component of the motion and the y-component of the motion.

The button 'reset' halts the animation and returns the position of the object to the starting point, but the settings are kept. 'Reset all' preserves nothing; it resets to the same state as when the webpage loaded.

Evolution of the display

The motion of the object is frictionless.

As stated above, the force is a proportional centripetal force. A proportional centripetal force is very symmetrical and the motion under the influence of that force has distinctive properties.

When the force that is present is a proportinal centripetal force all trajectories, circular and ellipse-shapep, have the same period of revolution.

In the case of motion determined by a proportional centripetal force the motion can be decomposed in two perpendicular oscillations. When the force that is exerted is exactly proportional to the distance to the center then the resulting motion is harmonic oscillation. Harmonic oscillation has the following property: the period is independent of the amplitude.

This property of harmonic oscillation propagates to the properties of the circumnavigating motion as depicted in the animation. For any trajectory, large amplitude or small amplitude, circular or ellipse-shaped, the period of circumnavigation is the same. The obvious choice of rotating coordinate system is the one that matches that amplitude-independent period.

Decomposition of the motion

Check the boxes for 'traces' and 'circle and epi-circle'. Then you see another elegant way of decomposing the ellipse-shaped trajectory in two components: a circle and an epi-circle. The center of the epi-circle moves in uniform circular motion around the central axis, the object moves in uniform circular motion along the epi-circle. When the overall rotation is counterclockwise (as in this example) then the motion along the main circle proceeds counterclockwise and the motion along the epi-circle proceeds clockwise.

Eccentricity

The motion along the epi-circle represents the eccentricity of the trajectory.

Transformation to a co-rotating coordinate system removes the motion along the main circle; the eccentricity remains. Also, note that as seen from a co-rotating point of view the motion along the epi-circle cycles twice for every cycle of the system as a whole.

The most efficient way to describe the acceleration with respect to the co-rotating system is to follow the decomposition in circle and epi-circle. Check the box for 'Coriolis & centrifugal'. The centrifugal vector is proportional to the distance to the central axis of rotation, the Coriolis vector represents the acceleration that corresponds with the uniform circular motion along the epi-circle.

Similar for all directions of motion

A defining characteristic of the Coriolis effect is that the acceleration with respect to the rotating system is the same for any direction of velocity.

As mentioned at the start: the animation is for the case where the magnitude of the centripetal force is proportional to the distance to the central axis of rotation. So whenever the object is circumnavigating slower than the rotating system the object experiences a surplus of centripetal force, and then this surplus pulls the object closer to the central axis of rotation.

Centripetal force and inertia

The rotation effect represented here arises from the centripetal force and inertia together.

When the object is pulled closer to the central axis of rotation the centripetal force is doing work. When the object has reached its point of closest approach its subsequent motion is dominated by its inertia; the object's velocity has become so large that its inertia carries it away from the central axis again. During motion away from the central axis the energy conversion is accounted for in the form of the centripetal force doing negative work.

Addition of another force

In this simulation there is only one force affecting the trajectory of the object; the centripetal force.

Imagine what would happen if there are other forces affecting the object. For example the object can be deflected with a gust of air. With another force added the dynamics will be determined by the sum of the two influences.

For example, a temporary gust of air directed against the object will shift it from one ellipse-shaped trajectory to another, and during that shift the Coriolis effect will continue to be at play.

Derivation of the effect

The following section is a copy of the derivation in the article about rotational-vibrational coupling

In the articles on this site I'm using the greek capital Ω (Omega) to refer to a constant factor, a non-changing angular velocity of a system as a whole; when the small greek letter ω (omega) is used it refers to the instantaneous angular velocity of some object. The instantaneous angular velocity of some object may fluctuate, depending on the circumstances. In the case of a proportional force the trajectory of the object can be expressed in terms of a function that contains a constant factor Ω.

Picture 1. Image

When the centripetal force is a proportional force, as in the case represented in the animation, the resulting trajectory can be describes as a superposition of two harmonic oscillations, at right angles to each other.

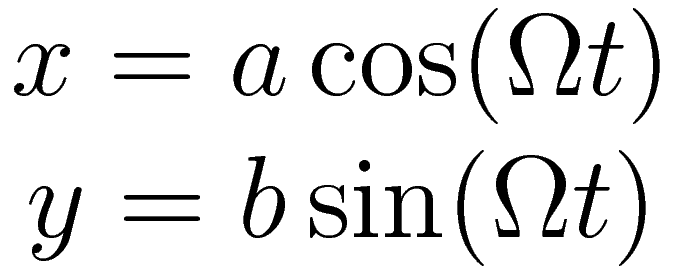
$\begin{matrix} x = a \cos(\Omega t) \\ y = b \sin(\Omega t) \end{matrix}$

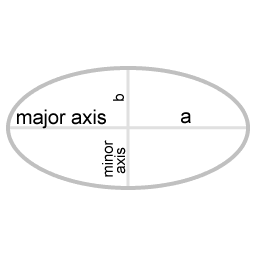
a	half the length of the major axis
b	half the length of the minor axis
Ω	360° divided by the duration of one revolution

To find exactly how the object moves as seen from a rotating point of view the parametric equation can be rearranged into the following two components:

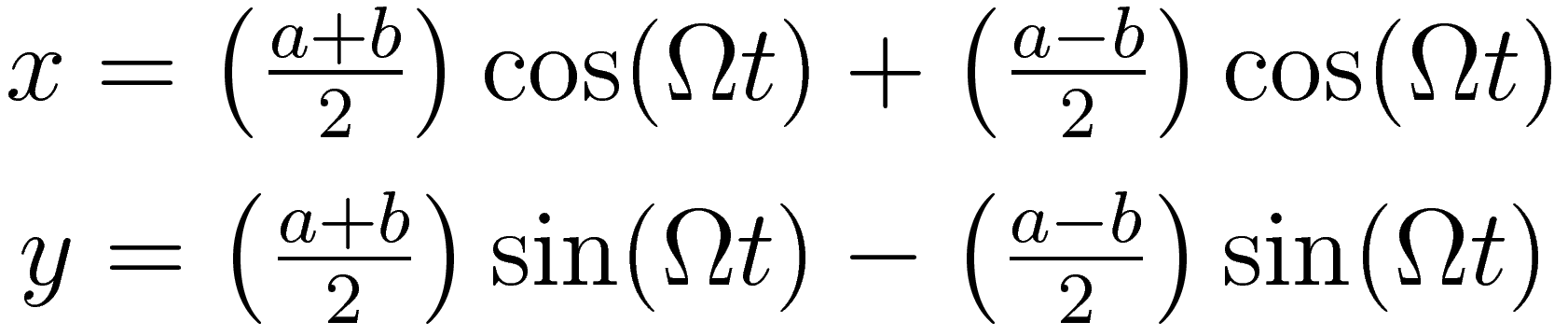
$\begin{matrix} x = \left(\frac{a+b}{2}\right)\cos(\Omega t) + \left(\frac{a-b}{2}\right)\cos(\Omega t) \\ y =\left(\frac{a+b}{2}\right)\sin(\Omega t) - \left(\frac{a-b}{2}\right)\sin(\Omega t) \end{matrix}$

Transformation to a coordinate system that is rotating with angular velocity Ω does the following: it subtracts the overall circular motion, and what is left is the eccentricity of the elliptical trajectory. The center of the eccentricity is located at a distance of (a + b) / 2 from the main axis of rotation.

The following parametric equation describes the motion with respect to the rotating coordinate system. (For simplicity the center of the epi-circle is used as the origin.)

$\begin{matrix} x & = & \ \ \ \left(\frac{a-b}{2}\right)\cos (2 \Omega t) \\[0.5em] y & = & - \left(\frac{a-b}{2}\right)\sin (2 \Omega t) \end{matrix}$

Magnitude of the Coriolis effect

We have confirmed that in the case of a proportional centripetal force the motion along the epi-circle is uniform circular motion. Hence the general expression for the centripetal acceleration a_c required to sustain uniform circular motion is applicable:

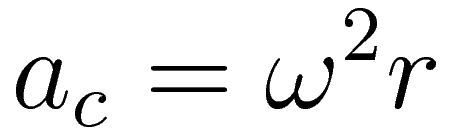
$a_c = \omega^2r$

(1)

Expression (1) will serve as the basis to arrive at an expression for the magnitude of the Coriolis effect for an object that has a velocity with respect to the rotating coordinate system.

Expression (1) contains a factor ω, which is angular velocity with respect to the center of the epi-circle at a distance r. To arrive at the expression for the Coriolis effect we need to convert both those factors.

In the case of motion along a circle we have the following general relation between (instantaneous) linear velocity v and angular velocity ω:

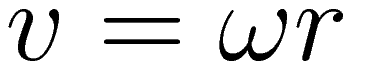
$v = \omega r$

(2)

We use (2) to change (1) into an expression that no longer contains the factor r for the radius of the epi-circle.

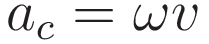
$a_c = (2\Omega)^2r$

(3)

And next we use the fact that the angular velocity ω with respect to the center of the epi-circle is twice the angular velocity of the rotating coordinate system with respect to the inertial coordinate system: ω = 2Ω

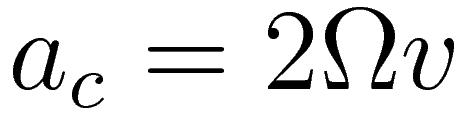
$a_c = 2\Omega v$

(4)

This 2Ωv acceleration relative to the rotating coordinate system is at all times perpendicular to the velocity. It's perpendicular because when the centripetal force is proportional the eccentricity is uniform motion along an epi-circle, and in the case of uniform circular motion the acceleration is at every point in time perpendicular to the velocity.

About the three factors in '2Ωv':
The factor '2' is there because for every revolution of the rotating system the motion along the epi-circle completes two cycles. The factor 'Ω' is there because of the centripetal force. The angular velocity of the rotating coordinate system is chosen such that it matches the period of the rotating motion, and the period of the rotating motion is determined by the strength of the centripetal force. The velocity 'v' is there because a larger velocity relative to the rotating coordinate system corresponds to a larger radius of the corresponding epi-circle.

This interactive animation was created with the Javascript Library JSXGraph. JSXGraph is developed at the Lehrstuhl für Mathematik und ihre Didaktik, University of Bayreuth, Germany.

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.

Last time this page was modified: June 22 2024