Rotational-vibrational coupling

Picture 1. Animation
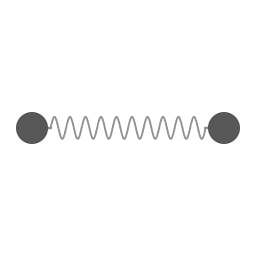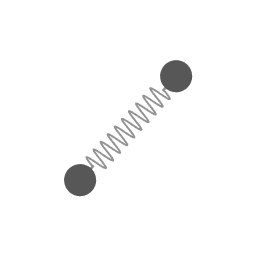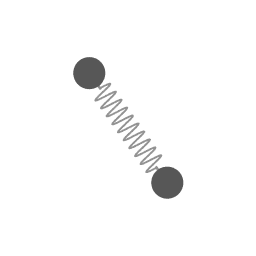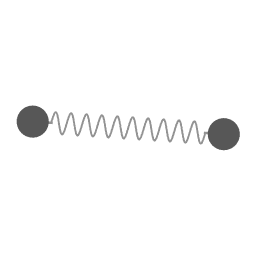
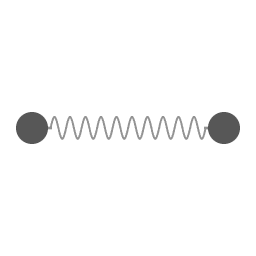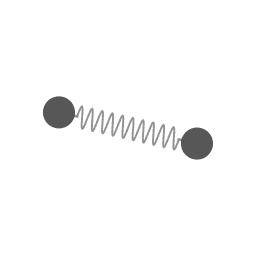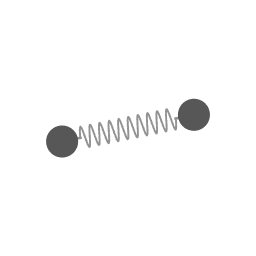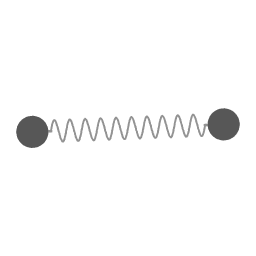
Two weights connected by a spring. There is a rotation around the common center of mass, and a coupled oscillation in radial distance and angular velocity.

Rotational-vibrational coupling occurs when there is a 1:2 ratio of rotation frequency of an object and a natural internal vibration frequency. The animation on the right shows the simplest example of this phenomenon. The motion depicted in the animation is for the idealized situation that the force exerted by the spring is proportional to the amount of extension. Note that in this demonstration the spring isn't alternating between pulling and pushing, the spring is exerting a contracting force all the time.

If some friction effect would drain all kinetic energy from the circumnavigating masses then the idealized spring would contract all the way down to zero length. The animation depicts the idealized case of frictionless motion.

In molecular physics it is recognized that there is a coupling of rotational and vibrational energy-levels. In molecular physics rotational-vibrational coupling is also called rovibronic coupling and Coriolis coupling. The physics of actual diatomic molecules is more complicated than the example in the animation, but because of its simplicity the animation is useful for illustrating the basic principles.

Energy conversions in rotational-vibrational coupling.

Picture 2. Animation
The motion of animation 1 mapped in a coordinate system that is rotating at a constant angular velocity.

Picture 3. Animation
Harmonic oscillation; the restoring force is proportional to the distance to the center.

During the phase in the cycle that the spring pulls the two weights closer to the center of rotation the angular velocity increases; the centripetal force is doing work, converting strain energy that was stored in the spring to kinetic energy of the weights.
At some point contraction ends and the weights swing wide again. As the distance of the weights to the central axis of rotation increases kinetic energy is converted to strain energy of the spring. The angular velocity decreases during this phase, and from a certain point on there is a surplus of centripetal force. Eventually the surplus of centripetal force starts a new phase of contraction.

Analogy with harmonic oscillation

Animation 2 provides a clearer view on the oscillation of the angular velocity. The motion as seen from a rotating point of view looks remarkably regular and symmetrical. It is in fact very regular; I will come to that further on in the article.

Harmonic oscillation is a cyclic process of energy conversion. When a harmonic oscillation is at its midpoint then all the energy of the system is kinetic energy. When the harmonic oscillation is at the points furthest away from the midpoint all the energy of the system is potential energy. The total energy of the system is conserved, but its form is oscillating back and forth between kinetic energy and potential energy.

In the motion pattern depicted in animation 2 there is, just as in the case of simple harmonic oscillation, a back and forth conversion between kinetic energy and potential energy. When the spring is at its maximal extension the potential energy its largest, when the angular velocity is at its maximum the kinetic energy is at its largest. The total energy of the system is conserved.

(With a real spring there is friction involved. With a real spring the vibration will be dampened and the final situation will be that the masses circle each other at a constant distance, with a constant tension of the spring. That is, in the final situation the ratio of kinetic energy to potential energy will be 1:1 .)

For a discussion of the role that momentum plays, see note on momentum

Mathematical derivation

Picture 4. Image

The motion of the circling masses is planar.
I'm applying the following simplifications: I'm taking the spring itself as being weightless, and I'm taking an idealized spring; the centripetal force increases in exact proportion to the amount of stretch. That is, in this simplification the amount of centripetal force is exactly proportional to the distance to the center of rotation. I will refer to this special case as 'proportional force'

The motion of the weights in two dimensions of space can be decomposed in two harmonic oscillations, perpendicular to each other.

The following parametric equation of the position as a function of time describes the motion of the circling masses. The parametric equation provides a complete description: it describes the shape of the trajectory and the velocity at each point in time.

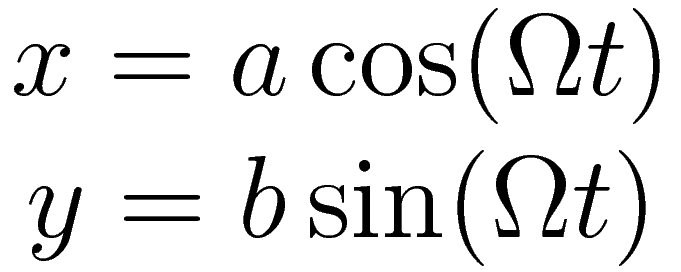
$\begin{matrix} x = a \cos(\Omega t) \\ y = b \sin(\Omega t) \end{matrix}$

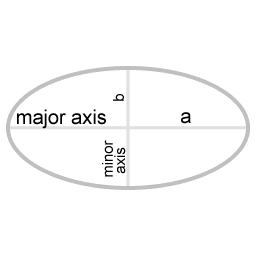
a	half the length of the major axis
b	half the length of the minor axis
Ω	360° divided by the duration of one revolution

In the articles on this site I'm using the greek capital Ω (Omega) to refer to a constant factor, a non-changing angular velocity of a system as a whole; when the small greek letter ω (omega) is used it refers to the instantaneous angular velocity of some object. The instantaneous angular velocity of some object may fluctuate, depending on the circumstances. In the case of a proportional force the trajectory of the object can be expressed in terms of a function that contains a constant factor Ω.

Picture 5. Animation
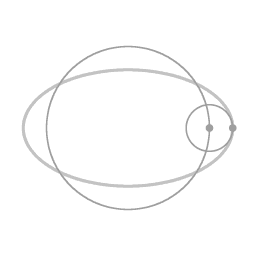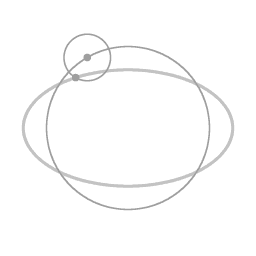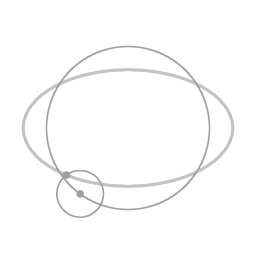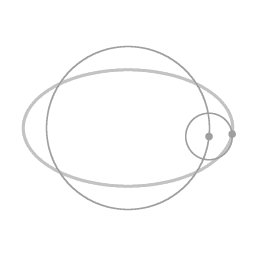
An ellipse-shaped trajectory (due to a proportional restoring force) can be seen as a circular motion (in this example counterclockwise), with the eccentricity as an epi-circle (clockwise).

Picture 6. Animation
The motion of animation 1 shown relative to a coordinate system that is rotating at a constant angular velocity.

The trajectory is eccentric. To find exactly how the object moves as seen from a rotating point of view the parametric equation can be rearranged into the following two components:

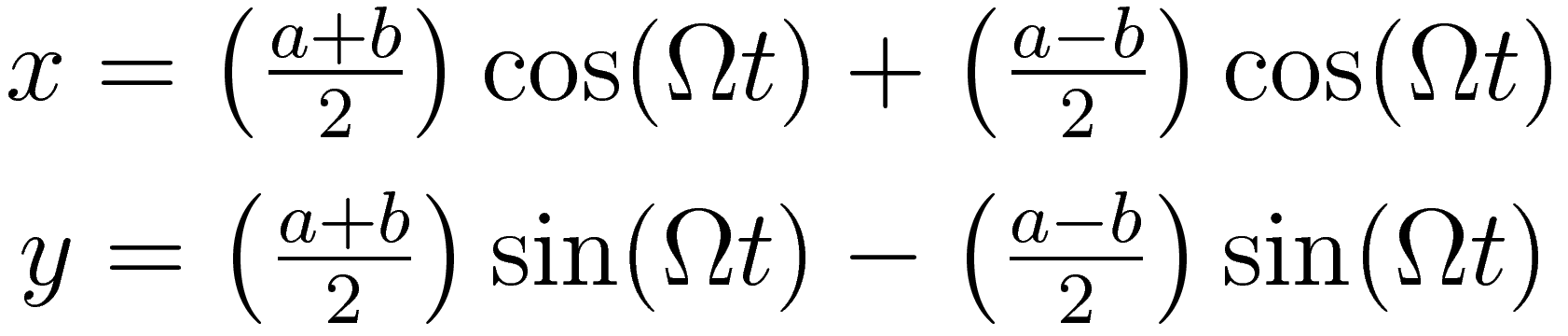
$\begin{matrix} x = \left(\frac{a+b}{2}\right)\cos(\Omega t) + \left(\frac{a-b}{2}\right)\cos(\Omega t) \\ y =\left(\frac{a+b}{2}\right)\sin(\Omega t) - \left(\frac{a-b}{2}\right)\sin(\Omega t) \end{matrix}$

Animation 5 depicts this rearrangement. There is an overall circular motion, combined with motion along an epi-circle. Both the motion along the overall circle (counterclockwise) and the motion along the epi-circle (clockwise) are uniform circular motion. This is a remarkable symmetry of motion under the influence of a proportional force; the eccentricity itself can be thought of as a uniform circular motion.

Transformation to a coordinate system that is rotating with angular velocity Ω does the following: it subtracts the overall circular motion, and what is left is the eccentricity of the elliptical trajectory. The center of the eccentricity is located at a distance of (a + b) / 2 from the main axis of rotation.

The transformation to a rotating coordinate system is of course to a particular one: the coordinate system in which the eccentricity of the ellipse-shaped trajectory is a circle around a fixed point. Here and everywhere else in this article (and everywhere else on this web site): whenever I refer to "transformation to a rotating coordinate system" I'm referring to the particular rotating coordinate system that matches the period of rotation.

$\begin{matrix} x & = & \ \ \ \left(\frac{a-b}{2}\right)\cos (2 \Omega t) \\[0.5em] y & = & - \left(\frac{a-b}{2}\right)\sin (2 \Omega t) \end{matrix}$

Animation 6 shows that relative to the rotating coordinate system the angular velocity along the epi-circle is 2Ω: it cycles twice for every cycle of the overall system. The radius of the eccentricity circle is (a - b) / 2.

Magnitude of the Coriolis effect

We have as starting point the general formula for the centripetal acceleration a_c that is required to sustain uniform circular motion:

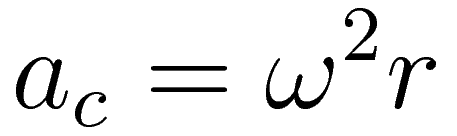
$a_c = \omega^2r$

(1)

Expression (1) will serve as the basis to arrive at an expression for the magnitude of the Coriolis effect for an object that has a velocity with respect to the rotating coordinate system.

Expression (1) contains a factor ω, which is an angular velocity with respect to the rotating coordinate system, and a distance r with respect to some center of angular velocity with respect to the rotating coordinate system. We want to replace both of them.

The end result will be an expression with the following two factors: angular velocity of the rotating system with respect to the inertial coordinate sytem, and the velocity of the object with respect to the rotating coordinate system.

In the case of motion along a circle we have the following general relation between (instantaneous) linear velocity v and angular velocity ω:

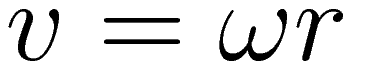
$v = \omega r$

(2)

We use (2) to change (1) into an expression that no longer contains the factor r for radial distance.

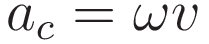
$a_c = (2\Omega)^2r$

(3)

And next we use the fact that the angular velocity ω with respect to the rotating coordinate system is twice the angular velocity of the rotating coordinate system with respect to the inertial coordinate system: ω = 2Ω

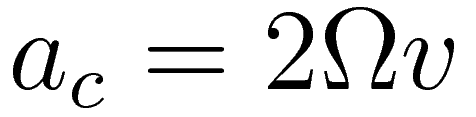
$a_c = 2\Omega v$

(4)

This 2Ωv acceleration relative to the rotating coordinate system is at all times perpendicular to the velocity. It's perpendicular because when the centripetal force is proportional the eccentricity is uniform motion along an epi-circle, and in the case of uniform circular motion the acceleration is at every point in time perpendicular to the velocity.

About the three factors in '2Ωv':
The factor '2' is there because for every revolution of the rotating system the motion along the epi-circle completes two cycles. The factor 'Ω' is there because of the centripetal force. The angular velocity of the rotating coordinate system is chosen such that it matches the period of the rotating motion, and the period of the rotating motion is determined by the strength of the centripetal force. The velocity 'v' is there because a larger velocity relative to the rotating coordinate system corresponds to a larger radius of the corresponding epi-circle.

Note on momentum
In the section 'Energy conversions in rotational-vibrational coupling' the dynamics is followed by keeping track of the energy conversions, rather than looking at the angular momentum. The advantage of following the energy conversions is that it focusus on causality.

Important as momentum is, momentum deals with spatial symmetry of the laws of physics, rather than with a cause-to-effect relation. This can be shown with the example of a cannon being fired. When a cannon is fired, the projectile will shoot out of the barrel towards the target, and the barrel will recoil. It would be wrong to suggest that the projectile leaves the barrel at high velocity because of the recoil of the barrel. While recoil of the barrel will always occur, (codified as the principle of conservation of momentum) it is not a causal agent. The causal mechanism is in the energy conversions: the explosion of the gun powder converts potential chemical energy to the potential energy of a highly compressed gas. As the gas expands, its high pressure exerts a force on both the projectile and the interior of the barrel. It is through the action of that force that potential energy is converted to kinetic energy of both projectile and barrel.

Similarly, in the case of rotational-vibrational coupling, the increase of angular velocity on contraction is consistent with the principle of conservation of angular momentum, but that should not be confused with conservation of angular momentum being a causal agent. In the case of rotational-vibrational coupling, the causal agent is the force exerted by the spring. The spring is oscillating between doing work and doing negative work. (The work is taken to be negative when the direction of the force is opposite to the direction of the motion.)
(back to article)

Next article:
Inertial oscillations

Major parts of this article have been uploaded by me to the wikipedia article about Rotational-vibrational coupling.
Wikipeda text is available under the terms of the GNU Free Documentation License

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.

Last time this page was modified: July 02 2022