Quantity of motion

Momentum and kinetic energy have in common that they are a measure of quantity of motion.

We take the following two postulates:

Time-reversal symmetry for perfectly elastic collision
Galilean invariance

Time reversal symmetry

When two objects of equal mass approach each other with equal velocity, and they collide with perfect elasticity, then their velocities will be reversed. That was a principle that from the 17th century on scientists relied upon in thinking about physical processes. Nowadays we have movie camera's, and we can play movies in reverse. We can readily see that in the case of a collision with perfect bounce we cannot discern whether the movie is being played forward or backward; perfectly elastic collision is symmetric in time.

(17th century scientists saw proof of the time-reversal symmetry in collision experiments. For instance, the case of two pendulums side by side so that when hanging still the bobs just touch. Then when both bobs are released from the same height, moving towards each other, they bounce back to the same height as the height they were released from. Of course, in coming to these conclusions the scientists had to assume that the small discrepancies they saw were due to friction only.)

Galilean invariance

To be a powerful set of principles the time-reversal symmetry must be paired with the principle that was introduced by Galilei, which nowadays is called 'Galilean relativity'. Imagine a set of large boats, all sailing along on perfectly smooth water. Each boat has a uniform velocity, all boats have some velocity relative to the other boats of the set. Then any experiment conducted onboard any of those boats will find the same laws of motion.

The 17th century scientist Huygens pointed out the following procedure: if you want to calculate the outcome of any collision, then transform to the coordinate system that is co-moving with the common center of mass, reverse the velocities and then transform back to the original coordinate system.

A more challenging case is where the mass of the two objects is unequal.

Common Center of Mass

In statics the Common Center of Mass (CCM) is an equilibrium point. Let two objects, with unequal mass, be connected by a stick with length L (for simplicity regard the stick as massless). Somewhere along the stick there will be an equilibrium point. If object 1 has twice the mass of object 2 then object 1 is twice as close to the Common Center of Mass as object 2.

The respective distances to the CCM can be notated as d₁ and d₂.
The system is in static equilibrium if m₂d₂ = m₁d₁ . That specifies a ratio between d₁ and d₂

If velocities are imparted to the objects then the CCM will remain motionless if:
m₁v₁ = m₂v₂

If a force is applied to both objects then the CCM will remain unaccelerated if:
m₁a₁ = m₂a₂

Derivation of laws from the invariance principles

I will discuss only the case of motion along a single line, in other words, the case of 1-dimensional motion. Two spherical objects with unequal masses move towards each other, they collide and then move apart again.

Galilean invariant notation

We can express their respective velocities as a v_a and v_b with respect to some chosen origin, but for the intended derivation there is a much better representation: expressing the velocities as motion with respect to the common center of mass.

V_r = the relative velocity between the two objects
V_c = the velocity of the CCM relative to some chosen origin

The relative velocity is taken as positive when the two object are approaching each other, and negative when the two objects are receding.

m₁	Mass of object 1
m₂	Mass of object 2
v₁	Velocity of object 1 relative to the CCM
v₂	Velocity of object 2 relative to the CCM

Then we have:

$v_1 = V_r \frac{m_2}{m_1 + m_2}$

(1)

$v_2 = - V_r \frac{m_1}{m_1 + m_2}$

(2)

v₁ and v₂ are in opposite directions, so one is added to V_c and the other is subtracted from it. You can readily verify that (v₁ - v₂) = V_r.

The benefit of this notation is that it literally embodies galilean relativity. Motion is expressed in terms of two separate entities: velocity relative to some chosen point of origin, and the relative velocity between the two objects. Thus the notation embodies that only the relative velocity matters for the physics taking place.

The notation enforces the demand that momentum is always conserved. Expressing velocities in terms of V_c and V_r is valid only if before and after a collision the CCM keeps the same velocity.

Arguably conservation of momentum and the principle of Galilean invariance are one and the same principle.

Kinetic energy

Whereas stating conservation of kinetic energy is very common the following property seems to be somewhat overlooked: kinetic energy is Galilean invariant. It's a necessary property: if kinetic energy would not be galilean invariant calculations would run into inconsistencies.

If kinetic energy is galilean invariant it must be possible to derive the conservation of kinetic energy from the invariance principles. So let's try that.

Let the total kinetic energy be called E_k. Kinetic energy is ½mv², but I have omitted the ½ because here it's non-essential. Then we have the following expression for the kinetic energy before the collision. (The symbol ∝ means 'is proportional to'.)

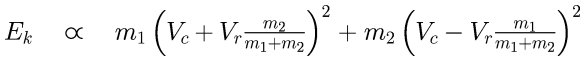
$E_k \quad \varpropto \quad m_1 \left( V_c + V_r \frac{m_2}{m_1 + m_2} \right)^2 \; + \; m_2 \left( V_c - V_r \frac{m_1}{m_1 + m_2} \right) ^2$

(3)

Because of the minus sign quite a few terms drop away against each other. After that cleanup the expression regroups as follows:

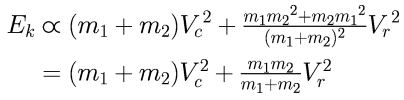
$\begin{align} E_k & = (m_1 + m_2) {V_c}^2 + \frac{m_1{m_2}^2 + m_2{m_1}^2}{(m_1 + m_2)^2} {V_r}^2 \\ & = (m_1 + m_2) V_c^2 + \frac{m_1m_2}{m_1 + m_2} V_r^2 \\ \end{align}$

(4)

After the collision

From symmetry it's immediately clear that in the expression for the total kinetic energy after the collision the same terms will drop away against each other, so after the cleanup and regrouping the expression will be the same as above.

There is the following limitation: while the derivation shows that there will be a conserved quantity that is proportional to the masses involved and to (V_r)², it doesn't go beyond that; it doesn't single out a particular expression for E_k.

Separate contibutions

It's interesting to see how readily the total kinetic energy can be separated into independent contributions: a component that correlates to the relative velocity (V_r) of two objects, and a component that correlates to their common velocity (V_c) with respect to some reference. This shows that kinetic energy satisfies Galilean invariance: the amount of kinetic energy that is involved in the collision process depends only on the relative velocity between the two objects.

Momentum and kinetic energy

What is the relation between momentum and kinetic energy?
Given that the corresponding conservation laws are both derivatives of the time symmmetry and Galilean invariance it appears that momentum and kinetic energy must in some sense be two sides of the same coin.

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.

Last time this page was modified: June 18 2017