Comparison of ballistics and inertial oscillations
This article relies on the reader being comfortable with the content
of the preceding article about inertial oscillations
The article consists of four sections, the first two sections discuss ballistics, the second two discuss inertial oscillations.
In the two sections covering ballistics I first discuss motion over a planar surface, in which case planar geometry is sufficient, then I discuss motion over the surface of a perfect sphere. Note that the geometry of the sphere's surface falls in the class of 2D geometries. Both the planar and the spherical case deal with motion over a surface; two coordinates suffice to cover the spatial degrees of freedom.
In the sections covering inertial oscillation I first discuss motion over the surface of a (very shallow) dish with a parabolic cross section, as described in the inertial oscillation article. It's important to note that in calculation a hybrid approach is customary. On one hand: for the purpose of geography the surface is approximated as a planar surface, on the other hand: the slope - the surface's deviation from flatness - gives rise to a centripetal force, and that centripetal force is the very factor that determines the trajectories.
The fourth case I discuss is inertial oscillation over the surface of an oblate spheroid; the surface of our Earth. Again, in meterological calculation a hybrid approach is customary. On one hand: for the purpose of geography the surface is approximated as a spherical surface, on the other hand: the slope - the Earth's deviation from sphericity - gives rise to a centripetal force, and as in the case of the parabolic dish model that centripetal force is the very factor that determines the trajectories.
Ballistics
Uniform motion with respect to an inertial coordinate system.

The blue circles represent pucks sliding over a flat surface. (The slightly larger circle represents a launching mechanim.
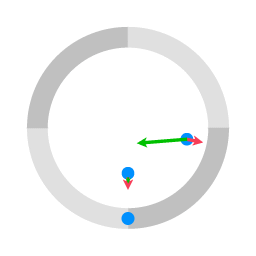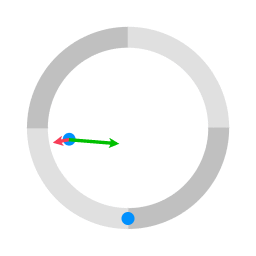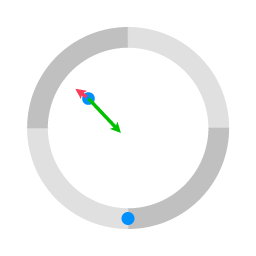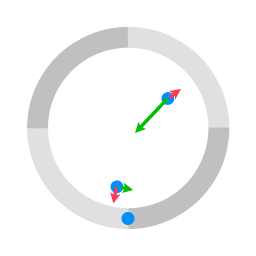
The green arrows represent the coriolis term of the equation of motion. The red arrows represent the centrifugal term.
In animation 1 the circle with four quadrants represents a rotating platform. The blue circles represent objects that are jettisoned to the other side, sliding frictionless along the surface. The blue circle that is co-rotating with the platform is the location of the launching mechanism. As there is no force in a direction parallel to the surface the blue objects follow a straight line trajectory.
Uniform motion with respect to a rotating coordinate system
In setting up an equation of motion for a rotating coordinate system (co-rotating with the platform) the centrifugal term and the coriolis term are added to the equation of motion. In the case of the rotating platform, there is no force acting on the pucks (at least not a force in a direction parallel to the surface), so the only terms in the equation of motion are the centrifugal term and the Coriolis term. When the vector of the centrifugal term and the vector of the coriolis term are added together, the resulting vector gives the acceleration with respect to the rotating coordinate system.
When motion is mapped in a rotating coordinate system the rotation is taken into account by adding the centrifugal term and the coriolis term. The centrifugal term and the Coriolis term are depicted in the following interactive animation: centrifugal effect. In this Java applet you can see the direction and the magnitude of the vector that represents the Coriolis term and of the vector that represents the centrifugal term.
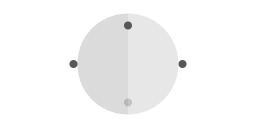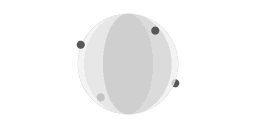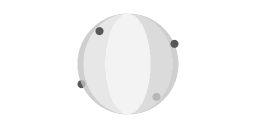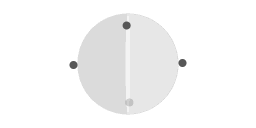
Motion along a great circle

Frictionless motion over the surface of a perfect sphere. The trajectory with respect to inertial space is a great circle, with a uniform angular velocity. Here, the plane of the great circle is tilted 45 degrees with respect to the plane of the equator.
In animation 3 an object is sliding frictionless over the surface of a sphere. The object moves along a great circle. The great circle that the object is moving along is tilted with respect to the sphere's equatorial plane. The sphere is rotating. Since the motion is thought of as frictionless motion, the fact that the sphere is spinning does not affect the direction in which the object is moving. As you can see, the time to complete a full great circle is equal to one period of the sphere's rotation.
The object is continuously traversing from the northern to the southern hemisphere and back. Another aspect of the tilted trajectory is that the satellite does not remain above the same longitude line. At the latitudes farthest away from the equator the satellite is "overtaking" the sphere. When the satellite traverses the plane of the equator it is "being overtaken" by the sphere. These changes of velocity are apparent; since the orbit is tilted the motion is geometrically projected. In calculations this projective geometry gives rise to a sine factor.
Frictionless motion over the surface of a perfect sphere. In this animation, the period of revolution of the objects is twice as long as the period of revolution of the sphere.
Animation 4 represents a variation on the motion pattern that is represented in animation 3. In animation 4 the objects move half as fast as in animation 3. The objects complete a full great circle it takes the sphere to complete two rotations. Consequently the objects are constantly being overtaken by the sphere.
Note that whenever the puck is moving parallel to a latitude line, it subsequently proceeds towards the equator.
Relevancy for ballistics
When a projectile is fired it enters a keplerian orbit around the center of mass of the Earth. (Of course, since a projectile moves through the atmosphere it experiences a lot of air friction.) To a (very rough) first approximation, a projectile that is fired will move relative to the Earth along a great circle. It follows that a projectile that is fired in westward direction along a latitude line wil subsequently proceed to the equator.
Motion in eastward and in westward direction
In this section I will discuss frictionless motion in eastward and in westward direction over the surface of a perfect sphere.
Motion over the surface of a non-rotating perfect sphere
Non-rotating sphere
The case of a non-rotating ice-sphere is analogous to frictionless motion over the surface of a non-rotating ice-floor. The small, dark disks represent ice hockey pucks. When the pucks separate they each have the same speed with respect to the surface. The pucks move along a great circle that is perpendicular to the longitude line that they start from. In other words: both pucks proceed towards the equator; if they keep going they will meet again on the other hemisphere.
Let me repeat why the pucks move along a great circle. The pucks rest on the surface of a perfect sphere. On a sphere the force of gravity is everywhere perpendicular to the surface. Since there is no force in a direction parallel to the surface there is nothing to cause deviation from motion in a straight line. On the surface of a sphere the mathematical counterpart of a straight line is a great circle.
The next step is to see how motion over the surface of a rotating perfect sphere is different from the non-rotating sphere case.
Rotating sphere

Similar launch as in animation 5, but on a rotating sphere

The same motion as animation 6, here as seen from a co-rotating point of view
The sphere rotates around its axis in a day. Initially the two pucks are held in place at 30 degrees latitude. When they are launched in opposite directions they proceed to move along the great circle that is tangent to the latitude that they are launched from. Note that while they have different velocities, they both proceed along the same great circle: the great circle that is tangent to the latitude line that they started from. The great circle that they move along is indicated with a "halo" around the sphere. Animation 6 represents the motion as seen from an inertial point of view, so the "halo" is stationary.
For reference, I need a concise unit of velocity. On Earth, an object that is located on the Equator, co-rotating with Earth, is circumnavigating the Earth's axis with a velocity of 1666 km/h. I will call that velocity one unit of velocity.
Animations 6 and 7 represent the case where the after their launch the pucks have a velocity of 0.25 unit of velocity with respect to the sphere, one puck in eastward direction with respect to the sphere, and the other puck westward with respect to the sphere. (On Earth 0.25 unit of velocity corresponds to a velocity with respect to the Earth's surface of about 440 kilometer/hour, about 280 miles/hour.) I will call the puck that moves westward with respect to the sphere 'the westward puck', and the puck moving eastward with respect to the sphere 'the eastward puck'.
Before the launch both pucks were circumnavigating the sphere's axis, counterclockwise as seen from the north pole. After the launch both pucks are still circumnavigating counterclockwise: the eastward puck has been boosted to a higher velocity, and the westward puck has had its velocity cut down. But they are still both circumnavigating counterclockwise.
Before the launch the westward puck was co-moving with the sphere at 30 degrees latitude, so it was circumnavigating the sphere's axis at 0.866 unit of velocity (0.866 is the cosine of 30 degrees). After the launch the westward puck is still circumnavigating in counterclockwise direction, but now at a velocity of 0.866 - 0.25 = 0.641 unit of velocity.
The eastward puck deviates from how it would move over a non-rotating sphere, deviating to the right of the direction of motion.
For the westward puck there is a deviation to the left as compared to how it would move over a non-rotating sphere.
Why deviation to the left?
So how come the westward puck deviates to the left as compared to how it would move over a non-rotating sphere? Isn't the Coriolis force supposed to deviate it to the right of the direction of motion? Well, in the equation of motion the Coriolis term does point to the right of the direction of motion, but the Coriolis term is not the only term in the equation. The equation of motion for a rotating coordinate system has two terms to accommodate the rotation of the coordinate system, the centrifugal term and the Coriolis term. Generally the centrifugal term is much larger than the Coriolis term, and that is the case here. In the case that is depicted in animations 6 and 7 the Coriolis term is swamped by the centrifugal term.
However, discussing the equation of motion for a rotating coordinate system does nothing to help physical understanding. So let me move to the physics taking place: prior to the launching of the pucks something was holding them in place, sustaining circumnavigating motion at 30 degrees latitude, co-moving with the entire rotating sphere. When the two pucks are released they proceed along the tangent great circle towards the equator.
Example: trajectory of a baseball
In baseball some pitchers can throw a fast ball that travels at about 150 km/hour (90 miles/hour). Fast as that is, at that velocity the outward centrifugal effect dominates the motion. So it matters whether the pitching is to the east or the west. Pitching in eastward direction: deflection to the right. Pitching in westward direction: deflection to the left. Of course, the rotation-of-Earth related deflection is too small to be noticable. Skilled pitchers can aim very precisely, but not that precise.
Inertial oscillations
Motion over the surface of a parabolic dish
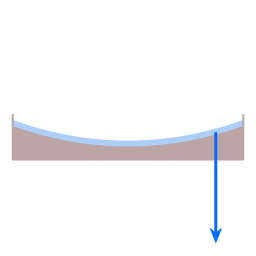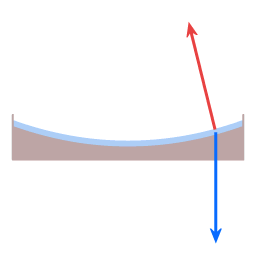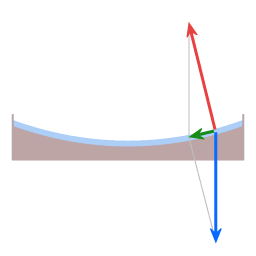
The blue arrow represents the force of gravity. The red arrow represents the normal force. The resultant force provides the required centripetal force. (The curvature of the dish is very much exaggerated.)

Frictionless motion along the surface of a parabolic dish.
The left side of animation 9 depicts the motion as seen from a non-rotating point of view. The right side depicts the motion as seen from a co-rotating point of view.
Categorizing deflection
It is important here to use a unambiguous definition of what is categorized as apparent deflection.
If a "deflection" is an artifact of mapping motion in a rotating coordinate system, then it is an apparent deflection. If a deflection is due to a force then it is independent of what coordinate system the motion is mapped in. For example: the retrograde motion of the planet Mars is apparent motion, but the orbit of Mars around the Sun is not.
There is an oscillation in the distance of the puck to the center of rotation, and an oscillation of the angular velocity of the puck. That pattern of oscillations is accounted for as due to work being done by a centripetal force, and this pattern of oscillation is the same when mapping the motion in an inertial coordinate system and when mapping the motion in a rotating coordinate system.
Motion over the surface of an oblate spheroid
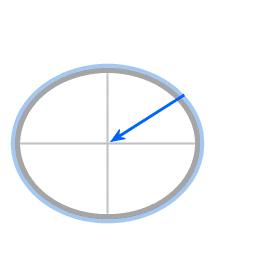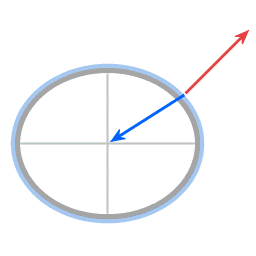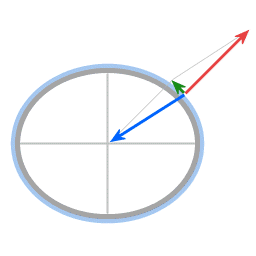
Forces in the case of an oblate spheroid.
Blue: gravitation
Red: normal force
The resultant force provides the required centripetal force.

Inertial oscillation over the surface of an oblate speroid.
Animation 11 represents inertial oscillations of an object that is in motion over the surface of a rotating oblate spheroid.
Animation 6 represents a situation without involvement of a poleward force. Then, when an object is moving in westward direction with respect to the Earth, the object deviates to the left. That is where motion without the presence of a poleward force, and motion under the influence of the poleward force literally diverge.
In the case of ballistics there is no force that acts in a direction parallel to the surface. (That is, to a first approximation. For a more detailed discussion, see the center of gravity section of the 'Equatorial bulge' article).
In the case of an oblate spheroid there is a poleward force, in which case there can be inertial oscillation.

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.
Last time this page was modified: June 18 2017