Special Relativity
1. Why laws of motion are possible
2. Special relativity
3. Unification: motion of objects and propagation of light
4. Acceleration in Minkowski spacetime
1. Why laws of motion are possible
The first relativity principle: Galilean relativity
In the history of physics, recognition of the central position of inertia has proceeded in stages. With the benefit of the current knowledge the Copernican revolution can be recognized as the first step to making inertia the prime organizing principle of dynamics understanding. (Here, I take 'Copernican revolution' in its widest possible sense: the revolution in thinking about motion that was completed by Newton's work.)
Galilei pointed out why it is possible to home in on laws of motion. Imagine you are in a cabin of a boat that is in motion over perfectly smooth water. I will call this particular boat the test boat. The test boat does not accelerate in any way, it is in uniform motion. You are on the test boat, juggling, or you are throwing darts, or something like that. (Galilei used other examples.) Galilei argued: no matter the velocity of the test boat, the skill for juggling the balls or throwing the darts is the same. There is a large range of circumstances that are different (boats having a velocity relative to each other), where as far as juggling is concerned things are the same for each separate boat. To become a skilful juggler is the acquirement of implicit knowledge (motoric knowledge) of how to work with the properties of motion.
The grid of the dartboard serves as a reference, the darter's aim is with respect to that reference system. One layer of 'the same' is that it does not matter where in space the dartboard is positioned, or in what direction the dartboard is facing; the properties of motion are the same. A second layer is that given a state of unaccelerated motion of the test boat its velocity relative to other boats does not matter either, the properties of motion as experienced on the test boat are always the same.
Symmetry of inertia
If you exert a force on an object, causing it to accelerate, then for all directions the same force results in the same acceleration; the isotropy of inertia. (Isotropy = same in all directions). For all locations and orientations in space, inertia is symmetrical. Likewise, for all uniform velocities, inertia is symmetrical. Imagine the opposite: imagine that inertia would be erratic, changing from place to place and from one instant to another - motion would be lawless then. But inertia is extremely symmetric. Formulating laws of motion is a fruitful undertaking because of the extensive symmetries of inertia.
A theory of motion describes the properties of inertia; in order to formulate a theory of motion it is necessary to have a way of embodying the symmetries of inertia. When a mathematical theory of motion was formulated, culminating in the work of Isaac Newton, embodying these symmetries was straightforward: euclidean space has the same symmetries as inertial space.
In retrospect we can recognize that the Copernican revolution changed the role that geometry played in physics. For the ancients the geometry was an instrument for describing shapes, the trajectory of a planet was thought of as a shape, and this shape was described by geometry. But in newtonian dynamics the euclidean geometry plays a much more profound role. In Newtonian dynamics inertia is the prime organizing principle and euclidean geometry is appropriate because it perfectly models the symmetries of inertia. In retrospect we can recognize that the act of using euclidean geometry as instrument for describing motion is actually the adoption of a physics theory.
Equivalence class of coordinate systems
The euclidean space is represented with a coordinate system (a coordinate grid). A coordinate system has a zero point and it has orientation. The comprehensive representation of the symmetries of inertial space must be specified as an equivalence class of coordinate systems.
Linear transformations
The symmetry demands narrow down the transformations to the following:
- Transformations between coordinate systems that are at an angle with respect to each other
- Transformation between coordinate systems that are translated with respect to each other
- Transformations between coordinate systems that have a uniform velocity relative to each other
For any object that is in inertial motion there is a coordinate system that is co-moving with that object. A coordinate system that is co-moving with an object in inertial motion is an inertial coordinate system. What that means is that the law that describes velocity addition of pairs of objects and the law that describes the transformation between inertial coordinate systems are one and the same law.
2. Special relativity
The special theory of relativity is, like Newton's laws of motion, a theory of motion: it deals with relations between space, time and matter.
As is the case with Newton's laws of motion, special relativity uses the phenomenon of inertia as the prime organizing principle of dynamics understanding, but on a more profound level. The purpose of this article is to demonstrate that.
synchronization procedure

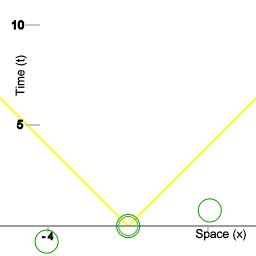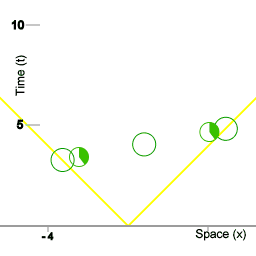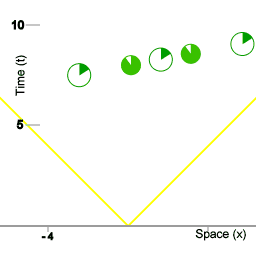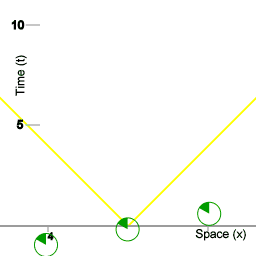
Three clocks.
Picture 1 represents three clocks, counting time. To keep those clocks perfectly synchronised you need a way of disseminating time. One way is to use pulses of light, I will get to that later. The next animation shows the three clocks, with smaller clocks shuttling between them.
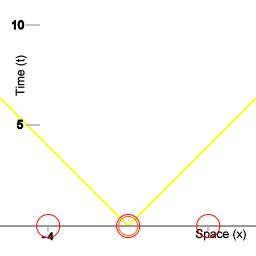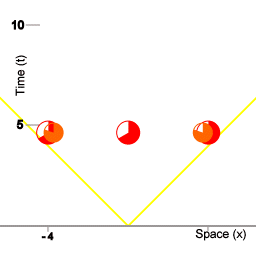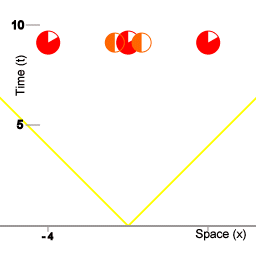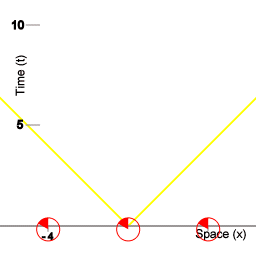
Three spaceships and a procedure to maintain synchronised fleet time.
Animation 2 represents a spacetime diagram. The yellow lines represent the worldlines of pulses of light that are emitted at t=0. The consecutive frames of the animation combined represent a single diagram.
An observer can always define his own position as the origin of a coordinate system to map the positions of other objects, such as the ships of a fleet of spaceships. In the animations of this article the fleet consists of three ships, but it can be any number of ships, and those ships can be regarded as forming a grid. That grid provides a coordinate system to assign a coordinate distance and a coordinate time-lapse between two events.
Each ship of the fleet logs the events taking place at its spatial coordinate, recording at what point in fleet time the event took place. The ships of the fleet communicate these logs to each other and on each ship of the fleet the information in the received logs can be put together in a comprehensive spacetime mapping of the events. Animation 2 is an example of such a comprehensive mapping.
The red circles represent clocks onboard the ships, counting time. The two orange circles represent miniclocks shuttling back and forth between the ships of the fleet, the miniclocks are used for a procedure to maintain synchronised fleet time. The synchronization procedure employed here relies on the isotropy of inertia. The ships of the fleet take care that every time the miniclocks are sent on their journey they are in both directions propelled with equal force. (More precisely: all the mini-clocks have the same mass, and in propelling each miniclock the ships of the fleet take care to impart the same amount of kinetic energy each time.)
The ships of the red fleet are 4 units of distance apart. Here, 4 units of distance means that as measured by the clocks of the fleet pulses of light take 4 units of time to propagate from one ship to another. In this article, distance is measured in terms of time: the amount of transit time of pulses of light. In this animation the miniclocks take 5 units of fleet time to travel from one ship to another, so their velocity relative to the fleet is 4/5th of the speed of light.
Time dilation
The animation depicts special relativity's prediction for this case that during the journey from one ship to another the miniclocks count 3 units of proper time. (Note that the time dilation doesn't prevent the synchronization. The amount of time dilation is perfectly predictable, so it can be accounted for.)
Over the course of a complete synchronization cycle you see the red clocks go round 10 times. That is, for the red clocks 10 units of time elapse. Conversely, you see the orange clocks go round 6 times; for the shuttles a complete cycle takes 6 units of shuttle time.
Transmission delays not fundamental
It's important to note that transmission delays play no part in special relativity. They must be accounted for, of course, in order to assemble a comprehensive spacetime mapping, but the substance of special relativity begins only after transmission delays have been taken into account. In order to get the relativistic effect in focus the animation is designed to avoid observational differences that arise from transmission delay.
No explanation
Relativistic physics does not provide an explanation as to how and why time dilation occurs. The starting point of relativistic physics is to assume that this is how things are, and the content of the theory consists of working out the ramifications of this assumption. The justification of the assumption is in the success of relativistic theory in applied physics.
Minkowski spacetime geometry
The conceptual shift in the transition from classical dynamics to the spacetime of special relativity is a shift from euclidean space and time to Minkowski spacetime.
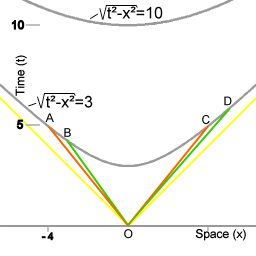
The chrono-geometry of spacetime intervals.
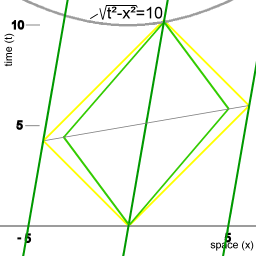
The line on which the points A, B, C, and D are grouped connects all the points in spacetime that have in common that for an object moving with uniform velocity from point O in spacetime to any point on that line, 3 units of proper time elapse. For instance, the lines OA and OC in image 3 correspond to the wordlines of the miniclocks in animation 2.
Spacetime interval
The concept of spacetime interval in Minkowski spacetime is somewhat analogous to the concept of radial distance in Euclidean space. In Euclidean space with 2 dimensions of space there is the relation:
Which is of course Pythagoras' theorem.
The radial distance between two points is an invariant, in the sense that it is independent of the particular choice of mapping a space with a cartesian coordinate system. More precisely, radial distance between two points is invariant under a coordinate transformation that corresponds to a spatial rotation.
In this article the word 'space' is used in a very abstract sense, in a meaning that is quite different from the everyday meaning of the word. In this article, everything is described in terms of time. Spatial distance is measured in terms of the amount of time that it takes light to cover the distance. Both time and spatial distance are counted in units of time.
The invariant spacetime interval of Minkowski spacetime geometry embodies a relation between space and time. The size of the spacetime interval is counted in units of time: the proper time as measured by co-moving clocks. The standard symbol for proper time is τ (the Greek letter 'tau'.)
The radical difference is the presence of the minus sign.
When represented geometrically, the spacetime interval is associated with a hyperbola curve, as depicted in image 3, whereas radial distance in Euclidean space is of course associated with a circle. Note that image 3 represents a mapping of a Minkowski space onto Euclidean space, rather than representing a Minkowski space directly.
Physical consequences
The shuttles are going back and forth between the ships of the red fleet. Each time they return to the ship that they came from and dock there they are still the same size as when they left. Space would be very strange indeed if returning from a journey you would find yourself to be smaller than when you left.
Now to the physical effect that does occur: the effect on elapsed time
The shuttles are taking a path that is not the spatially shortest path. Whenever that happens then on rejoining an object that did move along the spatially shortest path less proper time has elapsed for the traveller.
Metric of Minkowski spacetime
The measure of distance between two points in Euclidean space that is invariant under a rotation of the mapping coordinate system is called 'the metric of Euclidean space'.
In the case of Minkowski spacetime it is common to refer to its properties as 'geometry of Minkowski spacetime'. (A more accurate expression would be 'chrono-geometry of Minkowski spacetime', but that expression is rarely used.) By analogy with the concept of a metric in Euclidean context the formula for the invariant spacetime interval is referred to as 'the metric of Minkowski spacetime'.
The expression 'metric of Minkowski spacetime' is common usage, but because of the difference with the general concept of a metric it is also referred to as a 'pseudo-metric'. This signals that while in mathematical expressions the pseudo-metric performs exactly the same function as a metric, it is fundamentally different from a metric.
The concept of a metric can be applied in many different geometric contexts; A simple example of a metric is the metric of the way that in the game of chess the King moves around. To go from one corner to another along a column or a row takes 7 steps, and to go diagonally also takes 7 steps. That metric is an example of a non-euclidean metric, for Pythagoras' theorem does not apply.
The metric of Minkowski spacetime, with the square of one dimension being subtracted from the square of another dimension, is unexplained. For the question of how the structure of space and time can be like the way it is there is no established theory. At present, the Minkowski spacetime geometry must be assumed in order to be able to formulate a theory at all.
Spacetime interval
Special relativity implies that the spacetime interval is more fundamental than spatial distance. Special relativity implies that space cannot be thought of as an entity with an independent existence. Rather, physicists feel compelled to think of space as a sort of 3D silhouette of some more fundamental entity: the spacetime continuum, involving three spatial dimensions and one time dimension. Depending on how the spacetime is mapped spatial distances come out differently, in a way that is reminiscent of projective geometry.
Equivalence of different coordinate mappings
Three spaceships and a procedure to maintain synchronised fleet time.
The three dark green circles represent a fleet of spaceships. As in the first animations miniclocks are shuttling back and forth between the ships of the fleet, as part of a procedure to maintain synchronised fleet time. The trajectories of the green miniclocks correspond to the worldlines OB and OD in image 3.
The green fleet has a velocity with respect to the red fleet of 2/5th of the speed of light. The spacetime diagram in animation 4 represents how the motion of the green fleet is mapped in a coordinate system that is co-moving with the red fleet.
The metric of Minkowsk spacetime describes how everything will proceed for the green fleet. The central ship sends the miniclocks in opposite directions and each miniclock has a relative velocity of 4/5th of the speed of light with respect to the fleet. For each leg of the procedure, the miniclocks count 3 units of proper time, and the fleet clocks count 5 units of proper time for each leg of the procedure.
Symmetry
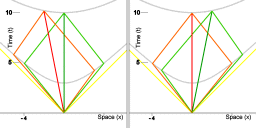
Image 5 shows spacetime diagrams that map both the procedure of the red fleet and the procedure of the green fleet. The diagram on the left shows a mapping of events in spacetime in a coordinate system that is co-moving with the green fleet, the diagram on the right shows a mapping of events in spacetime in a coordinate system that is co-moving with the red fleet.
In this particular case the synchronization procedure and its mapping in a spacetime diagram was introduced with the red fleet first, mapping the physics in a coordinate system that is co-moving with the red fleet. It could also have been introduced with the green fleet first, mapping the physics in a coordinate system that is co-moving with the green fleet. According to special relativity there is complete symmetry between the two coordinate representations.
Equivalence class of coordinate systems
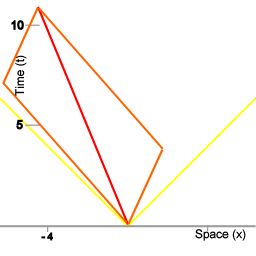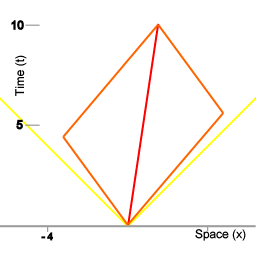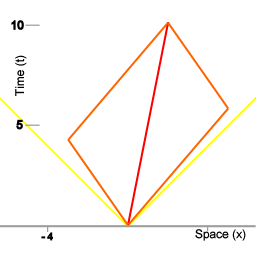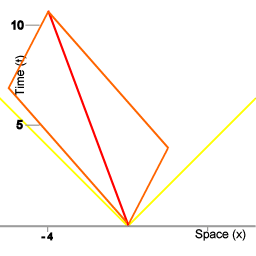
Equivalence class of coordinate systems.
In animation 6 the complete symmetry illustrated with image 5 is represented as an animation. Here, the sequence of frames is a sequence of coordinate systems with a velocity relative to each other. Each frame represents the same physics series of events: the synchronization procedure as outlined above. All individual frames of the animation represent the physics taking place equally well. Together the set of all frames in which the physics taking place is represented equally well constitutes an equivalence class of coordinate systems.
In particular the spacetime interval is the same in all spacetime mappings. On the other hand, in each frame simultaneity comes out differently relative to other frames.
Relativity of simultaneity
A tacit assumption in classical mechanics is that motion and simultaneity are distinct entities. That assumption does not carry over to special relativity. There is no inherent criterium to regard two events as simultaneous or not simultaneous. This is called the relativity of simultaneity.
While there is no inherent criterium for assigning simultaneity, there is an economy criterium. If you take as definition of simultaneity the synchronization procedure as above (synchronization that uses the symmetries of inertia as reference), then the physical laws, such as the equations for electromagnetism, are in their simplest form.
Comparison: luminiferous ether and Minkowski spacetime
Diagrams 7 to 10 represent cases of a synchronization procedure being applied. The yellow lines represent the worldlines of pulses of light.
In the previous examples the synchronization procedure used miniclocks. The advantage of that is that at each encounter you can see how much proper time has elapsed for the miniclocks during their journey, enabling you to check the fidelity of the synchronization. Every encounter it is checked that for each miniclock the same amount of proper time has elapsed during its journey.
When synchronizing with pulses of light that information isn't there: no comparison of transit time is possible.
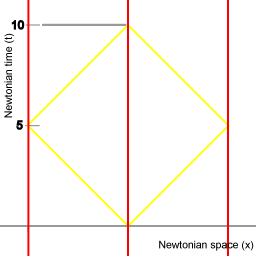
Picture 7. Diagram
The synchronization procedure in classical spacetime, using pulses of light. The procedure takes 10 units of time to complete. |
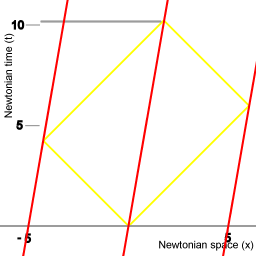
Picture 8. Diagram
The case of a fleet that has a velocity relative to the luminiferous ether: the procedure takes more than 10 units of time to complete. |
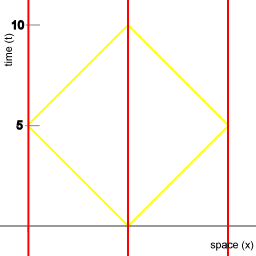
Picture 9. Diagram
The synchronization procedure in Minkowski spacetime. The coordinate system is co-moving with the fleet of spaceships. The procedure takes 10 units of time to complete. |
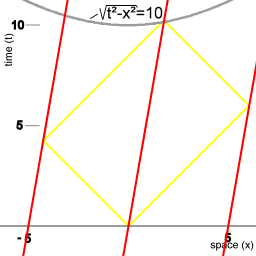
Picture 10. Diagram
The synchronization procedure mapped in a coordinate system that is moving relative to the fleet. After the procedure is completed 10 units of proper time have elapsed. |
Classical physics
Diagrams 7 and 8 represent what you expect to happen when the light signals are supposed to propagate in a medium, usually referred to as the luminiferous ether. If a fleet of spaceships has a velocity with respect to the luminiferous ether the overall pathlength of the light signals is longer, and the procedure will take more time than when the spaceships are stationary with respect to the luminiferous ether.
Minkowski spacetime
Diagrams 9 and 10 represent what you expect to happen when the environment is Minkowski spacetime. Every mapping of the procedure will indicate that 10 units of proper time will elapse. In other words, the synchronization procedure will not reveal anything about a velocity with respect to some background structure.
Einstein synchronization procedure
When pulses of light are used for synchronization of clocks the procedure is referred to as Einstein synchronization procedure. In the article, 'On the electrodynamics of moving bodies' in which Einstein introduced special relativity Einstein had introduced that procedure as a definition of simultaneity.
The diagrams illustrate in which environment the Einstein synchronization procedure is applicable. In space and time as envisioned prior to relativistic physics you expect the synchronisation procedure to take more time when the senders/receivers have a velocity relative to the luminiferous ether. That difference will give rise to inconsistencies, making the procedure unfit. In Minkowski spacetime, however, the Einstein synchronization procedure is the appropriate setup.
consequences for measurements of the speed of light
The only way to measure the speed of light is to set up a back and forth trip. If the environment is Newtonian space and time then you expect to find a different value for the speed of light, depending on the velocity of the measurement rig to the luminiferous ether.
Diagrams 8 and 9 illustrate how it works out in Minkowski spacetime. Different measurement setups, with a velocity relative to each other, will each find the same value for the speed of light. That means that the speed of light is an invariant.
Symmetric velocity time dilation

The situation is symmetrical. The red fleet and the green fleet have a velocity relative to each other, so for each unit of red time less than one unit of green time elapses, and for each unit of green time, less than one unit of red time elapses.
At time t=0 the two central ships of both fleets pass each other. At t=0, let the red ship emit a signal with a particular frequency, as measured in red fleet time. The green ship receives that signal, and that signal will be shifted to a lower frequency, as measured by green fleet time.
Conversely: at t=0 let the green ship emit a signal with a particular frequency, as measured in green fleet time. The red ship receives that signal, and that signal will be shifted to a lower frequency, as measured by red fleet time.
This type of time dilation is called symmetric velocity time dilation.
An example of that is the trajectories of the time-disseminating shuttles in the animations. At all times the shuttles have a velocity relative to each other, so there is a corresponding symmetric velocity time dilation. When the shuttles rejoin it is seen that among the shuttles there no difference in the amount of elapsed proper time.
Nonsymmetric velocity time dilation
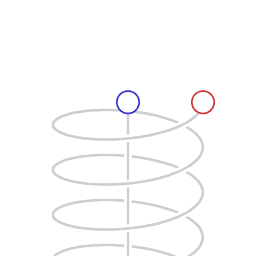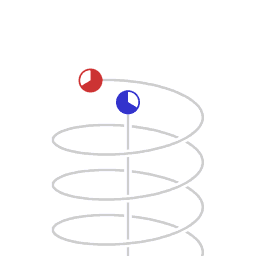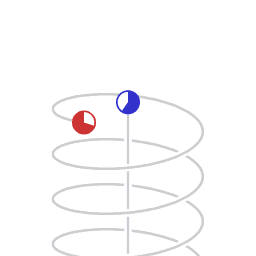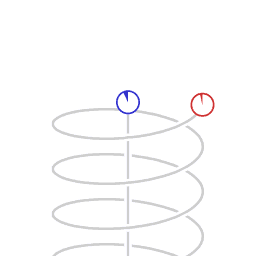
A straight worldline and a helical worldline.
Schematic representation of asymmetric velocity time dilation. The animation represents motion as mapped in a Minkowski spacetime diagram, with two dimensions of space, (the horizontal plane) and position in time vertically. The circles represent clocks, counting lapse of proper time. The Minkowski coordinate system is co-moving with the non-accelerating clock.
The clock in circular motion counts a smaller amount of proper time than the non-accelerating clock. Here, the difference in the amount of proper time that elapses is in a ratio of 1:2, which corresponds to a transversal velocity of 0.866 times the speed of light.
Any light emitted by the non-accelerating clock and received by the circling clock is received as a blue-shifted signal, in a ratio of 1:2. Any light emitted by the circling clock and received by the non-accelerating clock is received as a red-shifted signal, in a ratio of 2:1 .
In this situation, symmetry is broken, and there is a difference in amount of proper time that elapses.
3. Unification: motion of objects and propagation of light
The Principle of relativity of inertial motion
The synchronization procedure that the fleets use relies on the isotropy of inertia for objects in inertial motion. Both the red fleet and the green fleet are in inertial motion; for both fleet inertia is isotropic. Both the red fleet and the green fleet take care to transfer to the "left" and the "right" miniclock the same amount of kinetic energy. Since an identical amount of kinetic energy is transferred to the "left" and "right" miniclock (and given that they have identical mass), their velocity relative to the spaceship they were expelled from will be identical.
When Galilei formulated the principle of relativity of inertial motion the obvious supposition was that velocity-vectors add in the same way as vectors of euclidean space add. The assumption of galilean relativity is an assumption (a most intuitive one) about the chrono-geometric structure of space and time. At first sight it appears that galilean relativity is the only possible embodiment of the principle of relativity of inertial motion.
As discussed in the introduction: the symmetry demands that follow from the principle of relativity of inertial motion narrow down the transformations to the following:
- Transformations between coordinate systems that are at an angle with respect to each other
- Transformation between coordinate systems that are translated with respect to each other
- Transformations between coordinate systems that have a uniform velocity relative to each other
The revolution of special relativity lies in the recognition that there is yet another chrono-geometric structure that embodies the above set of symmetries: Minkowski spacetime. (Palash B. Pal has written up some very neat derivations, showing how both galilean relativity and special relavity satisfy the principle of relativity of inertial motion. Nothing but relativity (PDF-file 64 KB)
The limit of approaching the speed of light
In the animations the miniclocks have a velocity relative to the fleet of 4/5th of the speed of light. What happens at even faster velocities, approaching the speed of light? Subatomic particles such as protons and electrons can be accelerated to very close to the speed of light and expelled at that velocity. Then both as mapped in a coordinate system that is co-moving with the red fleet and in a coordinate system that is co-moving with the green fleet the particles move very close to the speed of light.
Light
Light itself is at the very extremal point. The physics of Minkowski spacetime is such that light always propagates away from any emitter with a velocity relative to that emitter of c, regardless of the velocity of that emitter relative to other emitters. Ultimately, synchronization with particles or synchronization with light relies on the same principle, the principle of inertia.
Fundamental unification: a single principle of inertia
When the synchronization procedure is performed both with pulses of light and with miniclocks the results will match up exactly.
In Minkowski spacetime, the members of the equivalence class of inertial coordinate systems have the following properties in common:
- Inertia of particles is isotropic
- Propagation of light is isotropic
The achievement of the special theory of relativity is placing motion of matter and propagation of light in a unified framework; both motion of particles and propagation of light are described by a single principle of inertia. Special relativity dissolves distinction between motion of particles and propagation of light. The key is Minkowski spacetime, the concept of Minkowski spacetime implies unification of the description of motion of particles and propagation of electromagnetic waves.
Thus, centuries after the Copernican revolution, special relativity goes a step further in recognizing inertia as prime organizing principle for dynamics understanding.
Transition: from newtonian to special relativity
The transition from newtonian dynamics to special relativity replaces one metric with another. Newtonian dynamics starts with the assumption that space is euclidean, that the dimension of time is euclidean, and that space and time are independent. Special relativity replaces these euclidean metrics with a single metric: the Minkowski metric.
In the next article, about the general theory of relativity, I will discuss that the transition from special relativity to its successor, the general theory of relativity, once again replaced the metric of spacetime.
4. Acceleration in Minkowski spacetime.
For an object moving in space the following is valid: it is possible to define a coordinate grid, with space dimensions and a time dimension, and all physics taking place can be mapped unambiguously in that coordinate grid. This coordinate grid also defines a 'plane of simultaneity'. What happens to that plane of simultaneity when the object proceeds through a phase of acceleration? Animation 5 suggests that during acceleration the object's plane of simultaneity sweeps through spacetime, settling on another orientation. That "sweeping" is just a metaphor; the 'plane of simultaneity' is only a mathematical abstract, there is no tangible physical counterpart. The point is that during a phase of acceleration it is not possible to map the surrounding space (and the objects in it) in a Minkowski diagram that is co-moving with the object that is accelerating. If you would try you get a mapping with intersecting planes of simultaneity, which is absurd.
Wikipedia has a very impressive animation: motion along a curvilinear worldline.
This is not a matter of whether special relativity can deal with acceleration. Special relativity can deal with acceleration perfectly well, provided you map the motion in an inertial coordinate system. Then the motion of that accelerating object is represented with a curvilinear worldline. The limitation of special relativity is that Minkowki spacetime diagrams are linear, and they extend infinitely. So you can't have Minkowski spacetime diagrams that are co-moving with an object that is accelerating, with the worldline straightened out, such diagrams are not self-consistent.
The animation suggests that something profound happens during physical acceleration. During physical acceleration, an object's relation to its surroundings changes.
Spacetime as a physical entity
In trying to understand special relativity common sense offers no guidance. Special relativity runs very much against expectation. Among the most counterintuitive aspects is the fact that special relativity attributes physical properties to spacetime. Minkowski spacetime is a physical entity, participating in the physics taking place. The nature of this participation is that the amount of proper time that elapses in travelling from a certain point A to a certain point B is path dependent. In travelling from point A to point B along a trajectory that is not the spatially shortest trajectory, a smaller amount of proper time elapses than when travelling along the spatially shortest path. This path dependence is key, and to emphasize its importance I'll put it in a box section.
Minkowski spacetime is a very interfering spacetime. Classical spacetime is, by comparison, a rather passive spacetime; if you travel in classical spacetime then the path you take is inconsequential. Not so in Minkowski spacetime: not taking the spatially shortest path has physical consequences.
Difference with ether theories
The major difference between ether theories and relativistic physics (arguably the only difference), is that in the case of relativistic physics velocity with respect to the assumed background structure (spacetime), does not enter the theory. It's important to observe the contrast: difference in spatial pathlength not only enters special relativity, it's crucial, and so is acceleration with respect to the background structure. But as a matter of principle velocity with respect to the background structure does not enter.
· Difference in spatial distance travelled: fundamental
· Velocity relative to Minkowski spacetime: does not enter.
· Acceleration with respect to Minkowski spacetime: fundamental.
Time derivatives: Position, Velocity, Acceleration
In classical dynamics the concepts Position, Velocity, and Acceleration are thought of as forming a sort of cascade. Velocity is the time derivative of Position, and Acceleration is the time derivative of Velocity. The "downstream" concepts are thought of as deriving from the upstream concept. The downstream entity being a derived entity implies that it must be dependent on its primitive.
- Position
-
- Velocity
-
- Acceleration
I will refer to the above scheme as the cascade model
Quite a few people rely on a tacit assumption that the cascade model carries over from classical dynamics to relativistic dynamics. Given that velocity with respect to inertial space does not enter special relativity it appears that the downstream concept, acceleration with respect to inertial space, cannot exist in special relativity either. But the tacit assumption is wrong: the cascade model doesn't carry over.
The twin paradox
There is that most famous paradox of all special relativity paradoxes: the twin paradox. It's interesting to examine why the twin paradox is surrounded with so much tension.
What if you expect that acceleration with respect the background structure does not enter special relativity? If that is the case then the twin scenario constitutes a true paradox. For those who perceive the twin scenario as a true paradox it appears as if there's something fundamentally wrong with relativistic physics. Such people argue that the twin paradox is a straightforward refutation of relativistic physics.
There are numerous discussions of the twin scenario, written for the purpose of showing that the twin scenario doesn't refute special relativity. Usually all that is shown is that the mathematics of special relativity is free from self-contradiction. But that doesn't address the actual issue. Those who argue that special relativity is illogical are tacitly assuming that the cascade model carries over from classical physics to relativistic physics.
As an example of extensive discussion that doesn't touch the actual issue, read the Usenet Physics FAQ discussion of the Twin scenario.
At the very end the author quotes a joke to express in what way his own discussion leaves him dissatisfied:
"Your Honor, I will show first, that my client never borrowed the Ming vase from the plaintiff; second, that he returned the vase in perfect condition; and third, that the crack was already present when he borrowed it."
In all, the discussion in the Physics FAQ presents something like three or four different "rebuttals". This weakens the case rather than strengthening it.
This is what makes special relativity counterintuitive: as a matter of principle velocity with respect to the background structure does not enter the theory, but acceleration with respect to the background structure is fundamental.

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.
Last time this page was modified: June 18 2017